题目内容
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.
如图①:直角三角形可以通过作斜边上的高把直角三角形分割成较小的三角形都与它相似,直角三角形是自相似图形.

解决问题:
(1)任意三角形都是自相似图形.请你在图②中完成分割,并作必要的标注.
(2)对于有一底角为60°,上、下底的比为1:2等腰梯形也是自相似图形,请你在图③中完成分割,并作必要的标注.
(3)现有一个矩形长AD=a,宽AB=b(a>b)是自相似图形.
①若分割成两块全等矩形,那么原矩形的长和宽应满足怎样的关系?
②若一次纵向分割成n块全等矩形,那么原矩形的长和宽应满足怎样的关系?
③如果要分割出纵向m块全等矩形和横向n块全等矩形,则原矩形的长a和宽b又应满足怎样的关系?直接写出答案.(用含b,m、n的代数式表示a)

如图①:直角三角形可以通过作斜边上的高把直角三角形分割成较小的三角形都与它相似,直角三角形是自相似图形.

解决问题:
(1)任意三角形都是自相似图形.请你在图②中完成分割,并作必要的标注.
(2)对于有一底角为60°,上、下底的比为1:2等腰梯形也是自相似图形,请你在图③中完成分割,并作必要的标注.
(3)现有一个矩形长AD=a,宽AB=b(a>b)是自相似图形.
①若分割成两块全等矩形,那么原矩形的长和宽应满足怎样的关系?
②若一次纵向分割成n块全等矩形,那么原矩形的长和宽应满足怎样的关系?
③如果要分割出纵向m块全等矩形和横向n块全等矩形,则原矩形的长a和宽b又应满足怎样的关系?直接写出答案.(用含b,m、n的代数式表示a)

考点:相似形综合题
专题:
分析:(1)作△ABC三边的中位线分割成的较小的三角形都与它相似,
(2)在等腰梯形内部作4个全等的等腰梯形即可;
(3)①根据矩形ABEF∽矩形FECD,得出AF:AB=AB:AD,再把a、b代入整理即可,
②根据每个小矩形都是全等的,得出边长为b和
a,再根据b:
a=a:b进行整理即可,
③先求出DN=
b,根据矩形FMND∽矩形ABCD,得出FD:DN=AD:AB,求出AF=a-
a,得出AG=
a,根据矩形GABH∽矩形ABCD,得出AG:AB=AB:AD,再代入得出a=
b;根据矩形DFMN∽矩形ABCD,得出FD:DN=AB:AD求出FD=
,得出AG=
,根据矩形GABH∽矩形ABCD,得出AG:AB=AB:AD,再代入得出a=
b.
(2)在等腰梯形内部作4个全等的等腰梯形即可;
(3)①根据矩形ABEF∽矩形FECD,得出AF:AB=AB:AD,再把a、b代入整理即可,
②根据每个小矩形都是全等的,得出边长为b和
| 1 |
| n |
| 1 |
| n |
③先求出DN=
| 1 |
| n |
| 1 |
| n |
| n-1 |
| mn |
|
| b2 |
| mn |
| na2-b2 |
| mna |
|
解答:解:(1)如图:作△ABC三边的中位线即可;

(2)根据题意画图如下:

(3)①∵矩形ABEF∽矩形FECD,
∴AF:AB=AB:AD,
即
a:b=b:a,
∴a=
b;
②每个小矩形都是全等的,则其边长为b和
a,
则b:
a=a:b,
∴a=
b;
③a=
b或a=
b;

由①②可知纵向m块矩形全等,横向n块矩形也全等,
∴DN=
b,
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD:
b=a:b,
解得FD=
a,
∴AF=a-
a,
∴AG=
=
=
a,
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即
a:b=b:a
得:a=
b;
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD:
b=b:a
解得FD=
,
∴AF=a-
,
∴AG=
=
=
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即
:b=b:a,
得:a=
b;
答:如果要分割出纵向m块全等矩形和横向n块全等矩形,则原矩形的长a和宽b又应满足a=
b或a=
b.

(2)根据题意画图如下:

(3)①∵矩形ABEF∽矩形FECD,
∴AF:AB=AB:AD,
即
| 1 |
| 2 |
∴a=
| 2 |
②每个小矩形都是全等的,则其边长为b和
| 1 |
| n |
则b:
| 1 |
| n |
∴a=
| n |
③a=
|
|

由①②可知纵向m块矩形全等,横向n块矩形也全等,
∴DN=
| 1 |
| n |
∵矩形FMND∽矩形ABCD,
∴FD:DN=AD:AB,
即FD:
| 1 |
| n |
解得FD=
| 1 |
| n |
∴AF=a-
| 1 |
| n |
∴AG=
| AF |
| m |
a-
| ||
| m |
| n-1 |
| mn |
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即
| n-1 |
| mn |
得:a=
|
∵矩形DFMN∽矩形ABCD,
∴FD:DN=AB:AD
即FD:
| 1 |
| n |
解得FD=
| b2 |
| mn |
∴AF=a-
| b2 |
| mn |
∴AG=
| AF |
| m |
a-
| ||
| m |
| na2-b2 |
| mna |
∵矩形GABH∽矩形ABCD,
∴AG:AB=AB:AD
即
| na2-b2 |
| mna |
得:a=
|
答:如果要分割出纵向m块全等矩形和横向n块全等矩形,则原矩形的长a和宽b又应满足a=
|
|
点评:此题考查了相似形综合,用到的知识点是相似多边形的判定与性质、中位线、自相似图形,关键是根据有关定义画出图形,做出相似多边形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,D为等腰直角△ABC的斜边AB上一点,点E在BC上,且DC=DE,求
如图,D为等腰直角△ABC的斜边AB上一点,点E在BC上,且DC=DE,求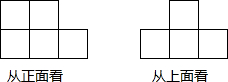 如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题:
如图所示的是由小立方体搭成的几何体从正面,上面看得到的平面图形,回答下列问题: