Question

【题目】如图，在中，，点，分别为，的中点，点在边上，连接，过点作的垂线交于点，垂足为点，且与四边形的周长相等，设，．

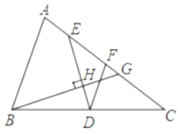
（1）求证：；

（2）若，求的值．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）根据中位线的性质和定义得DF =c，CF=b，结合△CDE与四边形ABDE的周长相等，得到CE=，可得EF的长，进而即可得到结论；

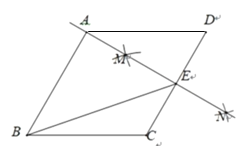
（2）连接BE，DG，过点A作AP⊥BG于P，过B作BM⊥DG于M，过E作EN⊥DG于N，证明四边形BMNE是平行四边形，易得BE∥DG，从而得到△ABE∽△FDG，进而得到FG=(bc)，再证∠BAP=∠DEF=∠PAC，得到△ABP≌△AGP，从而得AB=AG=c，结合CF=FG+CG，得到关于b，c的等式，即可得到结论．

（1）证明：∵点，分别为，的中点，

∴是的中位线，

∴，．

∵点为的中点，

∴．

∵与四边形的周长相等，

∴，

∴，

∴，

∴，

∴，

∴，

∴．

（2）解：连接，，过点作于，过B作BM⊥DG于M，过E作EN⊥DG于N，如图所示．

∵，

∴

∴，

∵△BDG和△EDG的底边为DG，

∴底边DG上的高BM=EN．

∵BM⊥DG，EN⊥DG，

∴BM∥EN，

∴四边形BMNE是平行四边形，

∴BE∥DG．

∵是的中位线，

∴，，

∴∠BAE=∠DFG．

∵BE∥DG，

∴∠AEB=∠FGD，

∴，

∴，

∴．

∵，

∴，

∵，

∴∠BAE=∠DFG=2∠DEF，

∴．

∵，，

∴，

∴，

∴．

∵，

∴∠APB=∠APG=90°．

∵AP=AP，

∴△ABP≌△AGP，

∴，

∴，

∴，

∴，

∴．