题目内容
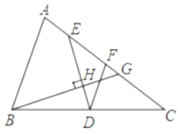
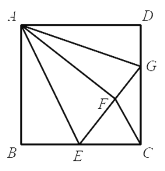
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
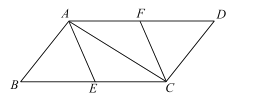
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
【答案】(1)见解析;(2)当![]() 时,四边形
时,四边形![]() 是正方形,理由见解析
是正方形,理由见解析
【解析】
(1)先证明![]() 得到
得到![]() ,
,![]() ,由点E,F分别是BC,AD的中点得
,由点E,F分别是BC,AD的中点得![]() ,
,![]() ,然后运用SSS证明
,然后运用SSS证明![]() 即可;
即可;
(2)易证四边形![]() 是平行四边形,再证明四边形
是平行四边形,再证明四边形![]() 是平行四边形,证明AE=EC得平行四边形
是平行四边形,证明AE=EC得平行四边形![]() 是菱形,由
是菱形,由![]() ,点
,点![]() 是
是![]() 的中点可证明菱形
的中点可证明菱形![]() 是正方形.
是正方形.
(1)证明:∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
∵点![]() 分别是
分别是![]() ,
,![]() 的中点
的中点
∴![]() ,
,![]() ,
,
∴![]()
∴![]()
(2)当![]() 时,四边形
时,四边形![]() 是正方形
是正方形
理由:
∵![]() ,
,![]()
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∵点![]() 分别是
分别是![]() ,
,![]() 的中点
的中点
∴![]() ,
,![]() ,
,
∴![]()
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() ,点
,点![]() 是
是![]() 的中点
的中点
∴![]()
∴平行四边形![]() 是菱形
是菱形
∵![]() ,点
,点![]() 是
是![]() 的中点
的中点
∴![]() 即
即![]()
∴菱形![]() 是正方形.
是正方形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目