题目内容
 (1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)
(1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)(2)观察(1)中所画图象,填空:当x满足:
(3)观察图形,填空:当0≤x≤3时,y最大值=
考点:二次函数的图象,二次函数的最值,二次函数与不等式(组)
专题:
分析:(1)将抛物线y=-x2+2x配方,求出顶点坐标,对称轴与x轴(y轴)的交点,画出图象.
(2)根据图象即可求得y>0时,x的取值;
(3)根据图象即可求得当0≤x≤3时,函数的最大值和最小值.
(2)根据图象即可求得y>0时,x的取值;
(3)根据图象即可求得当0≤x≤3时,函数的最大值和最小值.
解答:解:(1)∵抛物线y=-x2+2x=-(x-1)2+1,
∴顶点坐标为(1,1),开口向下,过原点,画图如下:

(2)由图象可知,0<x<2时,y>0.
故答案为0<x<2.
(3)当0≤x≤3时,y最大值=1,y最小值=-3.
故答案为1,-3.
∴顶点坐标为(1,1),开口向下,过原点,画图如下:

(2)由图象可知,0<x<2时,y>0.
故答案为0<x<2.
(3)当0≤x≤3时,y最大值=1,y最小值=-3.
故答案为1,-3.
点评:此题考查二次函数的图象与性质,二次函数的最值以及二次函数和不等式的关系.数形结合思想的运用是本题的关键.

练习册系列答案
相关题目
 如图:已知平行四边形ABCD中,K是BC上一点,且
如图:已知平行四边形ABCD中,K是BC上一点,且| BK |
| KC |
| 3 |
| 4 |
| BE |
| ED |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.
如图,BD⊥AC,CE⊥AB,垂足分别为点D和点E,BD与CE相交于点F,BF=CF.求证:点F在∠BAC的平分线上.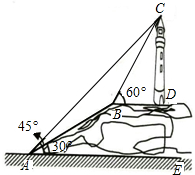 如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
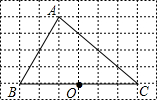 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.