题目内容
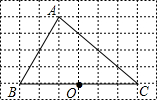 如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
考点:位似变换
专题:计算题
分析:(1)连结OA,分别取OA、OB、OC的中点A′、B′、C′,则△A′B′C′为所求;
(2)先利用勾股定理计算出OA═
,AC=4
,再利用位似的性质得到A′C′=
AC=2
,
=
=
,则OC′=
OC=
,OA′=
OA=
,所以AA′=
,CC′=
,然后计算四边形AA′C′C的周长.
(2)先利用勾股定理计算出OA═
| 17 |
| 2 |
| 1 |
| 2 |
| 2 |
| OC′ |
| OC |
| OA′ |
| OA |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
解答:解:(1)所作图形如图所示:

(2)OA=
=
,AC=
=4
,
∵△A′B′C′和△ABC位似,且位似比为1:2;
∴A′C′=
AC=2
,
=
=
,
∴OC′=
OC=
,OA′=
OA=
,
∴AA′=OA-OA′=
,CC′=OC-OC′=
,
∴四边形AA'C'C的周长=AC+CC′+A′C′+AA′
=4
+
+2
+
=6
+
+
.

(2)OA=
| 12+42 |
| 17 |
| 42+42 |
| 2 |
∵△A′B′C′和△ABC位似,且位似比为1:2;
∴A′C′=
| 1 |
| 2 |
| 2 |
| OC′ |
| OC |
| OA′ |
| OA |
| 1 |
| 2 |
∴OC′=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴AA′=OA-OA′=
| ||
| 2 |
| 3 |
| 2 |
∴四边形AA'C'C的周长=AC+CC′+A′C′+AA′
=4
| 2 |
| 3 |
| 2 |
| 2 |
| ||
| 2 |
=6
| 2 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:两个图形必须是相似形;对应点的连线都经过同一点;对应边平行.

练习册系列答案
相关题目
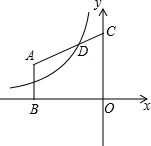 如图,点A在反比例函数y=
如图,点A在反比例函数y=| 3 |
| x |
| A、3 | B、4 | C、6 | D、9 |
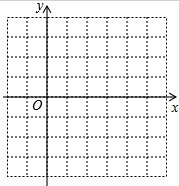 (1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)
(1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)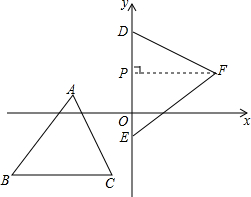 如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上.
如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上.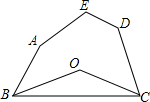 已知,如图,O是五边形ABCDE内一点,且∠OBC=
已知,如图,O是五边形ABCDE内一点,且∠OBC=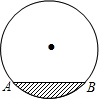 维修人员为更换一圆柱形的输水管道,需先确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面,若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
维修人员为更换一圆柱形的输水管道,需先确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面,若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.