题目内容
数轴上点A对应的数为1,点B到点A的距离为3,将线段AB沿数轴向右移动4个单位长度得到线段A′B′(点A的对应点为A′),则点B′对应的数为 .
考点:数轴
专题:
分析:根据两点间的距离公式可得点B对应的数,再根据平移的性质即可求解.
解答:解:∵数轴上点A对应的数为1,点B到点A的距离为3,
∴点B对应的数为-2或4,
∴当点B对应的数为-2时,将线段AB沿数轴向右移动4个单位长度得到线段A′B′(点A的对应点为A′),则点B′对应的数为-2+4=2;
当点B对应的数为4时,将线段AB沿数轴向右移动4个单位长度得到线段A′B′(点A的对应点为A′),则点B′对应的数为 4+4=8.
综上所述,点B′对应的数为2或8.
故答案为:2或8.
∴点B对应的数为-2或4,
∴当点B对应的数为-2时,将线段AB沿数轴向右移动4个单位长度得到线段A′B′(点A的对应点为A′),则点B′对应的数为-2+4=2;
当点B对应的数为4时,将线段AB沿数轴向右移动4个单位长度得到线段A′B′(点A的对应点为A′),则点B′对应的数为 4+4=8.
综上所述,点B′对应的数为2或8.
故答案为:2或8.
点评:本题主要考查了两点之间的距离,同时需要注意点在数轴上移动的特点,难度适中.涉及了分类思想的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
在-3,0,-2,-
四个数中最小的是( )
| 2 |
| A、-3 | ||
| B、0 | ||
| C、-2 | ||
D、-
|
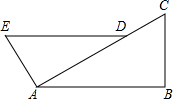 已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.
已知:如图,在Rt△ABC中,∠B=90°,AE⊥CA,且AE=BC,点D在AC上,且AD=AB,求证:DE∥AB.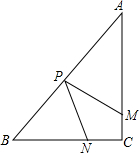 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).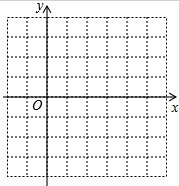 (1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)
(1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.) 如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.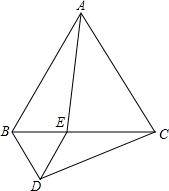 如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.