题目内容
11.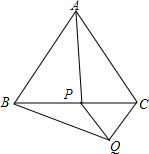 (1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.
(1)如图,在等边△ABC中,在BC边上任取一点P,过点P作AC的平行线,过点C作AB的平行线,两线交于点Q.求证:AP=BQ.(2)在上面的条件下,点P在BC边上任意运动,延长AP交BQ于点D,请画出图形,问AD与BD+CD之间是否存在确定关系?若存在,请指明这个关系,并证明你的结论;若不存在,请说明理由.
分析 (1)根据等边三角形的性质得到∠ABC=∠ACB=60°,AC=BC,根据平行线的性质得到∠CPQ=∠ACB=60°,∠PCQ=∠ABC=60°,推出△PCQ是等边三角形,得到CP=CQ,证得△ACP≌△BQC,根据全等三角形的性质即可得到结论;
(2)根据等边三角形的性质得到∠ABC=∠ACB=60°,AC=BC,由平行线的性质得到∠QCP=∠ABC=60°,同理,∠CPQ=60°,推出△PCQ为等边三角形,于是得到CQ=CP,推出△BCQ≌△ACP,根据全等三角形的性质得到∠CBQ=∠CAP,在AP上截取点E,使AE=BD,证得△BCD≌△ACE,由全等三角形的性质得到CD=CE,∠ACE=∠BCD,推出△CDE为等边三角形,等量代换即可得到结论.
解答 解:(1)∵在等边△ABC中,
∴∠ABC=∠ACB=60°,AC=BC,
∵PQ∥AC,
∴∠CPQ=∠ACB=60°,
∵CQ∥AB,
∴∠PCQ=∠ABC=60°,
∴△PCQ是等边三角形,
∴CP=CQ,
在△ACP与△BQC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACB=∠BCQ}\\{CP=CQ}\end{array}\right.$,
∴△ACP≌△BQC,
∴AP=BQ;
(2)AD=BD+CD,
∵△ABC是等边三角形,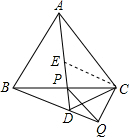
∴∠ABC=∠ACB=60°,AC=BC,
∵CQ∥AB,
∴∠QCP=∠ABC=60°,
同理,∠CPQ=60°,
∴△PCQ为等边三角形,
∴CQ=CP,
在△BCQ与△ACP中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCQ=∠ACB}\\{CQ=CP}\end{array}\right.$,
∴△BCQ≌△ACP,
∴∠CBQ=∠CAP,
在AP上取点E,使AE=BD,
在△BCD与△ACE中,
$\left\{\begin{array}{l}{BC=AC}\\{∠CBQ=∠CAP}\\{BD=AE}\end{array}\right.$,
∴△BCD≌△ACE,
∴CD=CE,∠ACE=∠BCD,
∵∠ACE+∠ECB=60°,
∴∠BCE+∠BCD=∠ECD=60°,
∵CD=CE,
∴△CDE为等边三角形,
∴CD=ED,
∴AD=AE+ED=BD+CD.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的性质,熟练掌握全等三角形的判定和性质是解题的关键.

| A. | (a+3)(a-3)=a2-3 | B. | (3b+2)(3b-2)=3b2-4 | ||
| C. | (3m-2n)(-2n-3m)=4n2-9m2 | D. | (x+2)(x-3)=x2-6 |
| A. | 0 | B. | 1 | C. | -1 | D. | 3 |
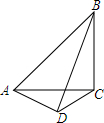 如图,△ABC中,AC=BC,∠ACB=90°,D为△ABC外一点,且AD⊥BD,求证:∠CDB=45°.
如图,△ABC中,AC=BC,∠ACB=90°,D为△ABC外一点,且AD⊥BD,求证:∠CDB=45°.