题目内容

15．已知$\sqrt{19}$的整数部分是a，（b-2）2$+\sqrt{c+3}=0$，则$\frac{3a-2c}{b}$的算术平方根为3．

分析 先分别求出a、b、c的值，再求出$\frac{3a-2c}{b}$的值，最后求出算术平方根即可．

解答 解：∵4＜$\sqrt{19}$＜5，
∴a=4，
∵（b-2）2$+\sqrt{c+3}=0$，
∴b-2=0，c+3=0，
∴b=2，c=-3，
∴$\frac{3a-2c}{b}$=9，
∴$\frac{3a-2c}{b}$的算术平方根是3．
故答案为：3．

点评 本题考查了估算无理数的大小，算术平方根，偶次方的应用，解此题的关键是能求出a、b、c的值．

练习册系列答案
相关题目
12．某市为了缓解交通压力决定建高架桥，A、B两个公司都希望承接这项工程．已知甲公司每个月可建160米高架桥，乙公司每个月可建240米高架桥，而且完成这项工程甲公司比乙公司要多用20个月．该城市政府需付给甲公司建筑费每月240万元，乙公司建筑费每月360万元．
（1）求该城市要建多长的高架桥？（用方程解决问题）
（2）该城市政府设计方案时，考虑可由每个公司单独做，也可以由两个公司合作建成，在建设过程中，政府需要派5名工程师到建筑工地里进行指导，建筑公司负担每人每月3000元的生活补贴费．你帮助该城市政府选择一种既省时又省钱的建设方案，并说明理由．（用方程解决问题）
6．如图：已知A（a，0）、B（0，b），且a、b满足（a-2）2+|2b-4|=0．
（1）如图1，求△AOB的面积；
（2）如图2，点C在线段AB上（不与A、B重合）移动，AB⊥BD，且∠COD=45°，猜想线段AC、BD、CD之间的数量关系并证明你的结论；
（3）如图3，若P为x轴上异于原点O和点A的一个动点，连接PB，将线段PB绕点P顺时针旋转90°至PE，直线AE交y轴Q，点Q，当P点在x轴上移动时，线段BE和线段BQ中，请判断哪条线段长为定值，并求出该定值．
3．解方程：
（1）（x+1）2=16；
（2）125（x-1）3=-64．
10．点（-4，3）向右平移3个单位长度，再向下平移2个单位长度后的坐标为（-1，1）；
点（3，-1）向左平移1个单位长度，再向上平移4个单位长度后的坐标为（2，3）．
20．解下列方程
（1）3（2x-1）-2（1-x）=0
（2）$\frac{2x-1}{3}$=$\frac{2x+1}{6}$-1．
7．一水库里有鲤鱼、鲫鱼、草鱼共2 000尾，小明通过多次捕捞试验，发现鲤鱼、草鱼的概率是51%和26%，则水库里有460尾鲫鱼．
4．若y2-2y+1+$\sqrt{x+y-1}$=0，则xy的值等于（　　）
A．0B．-2C．2D．6
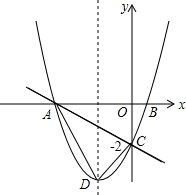5．已知抛物线y=ax2+bx+c与x轴交于A、B两点，交y轴于点C，点D为顶点且△ABC的是直角三角形，A点坐标为（-4，0），C点的坐标为（0，-2），直线y=kx+b经过A、C两点．
（1）求抛物线和直线的函数解析式；
（2）求四边形ABCD的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网