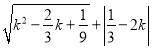题目内容
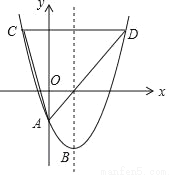
如图,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣4与y轴交于点A,顶点为B,点A的坐标为(0,﹣2),点C在抛物线上(不与点A,B重合),过点C作y轴的垂线交抛物线于点D,连结AC,AD,CD,设点C的横坐标为m.
(1)求这条抛物线所对应的函数表达式.
(2)用含m的代数式表示线段CD的长.
(3)点E是抛物线对称轴上一点,且点E的纵坐标比点C的纵坐标小1,连结BD,DE,设△ACD的面积为S1,△BDE的面积为S2,且S1•S2≠0,求S2=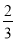 S1时m的值.
S1时m的值.
(4)将抛物线y=a(x﹣2)2﹣4沿x=2平移,得到抛物线y=a(x﹣2)2+k,过点C作y轴平行线与抛物线y=a(x﹣2)2+k交于点F,若CD与y轴交于点G,且CD=6,直接写出使AC=FG的点F的坐标.
练习册系列答案
相关题目


 B.
B.  C.
C.  D.
D. 
 B.
B.  C.
C.  D.
D. 
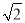 ≈1.4,
≈1.4, 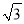 ≈1.7,结果保留整数】
≈1.7,结果保留整数】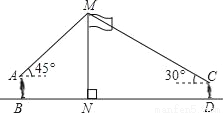
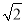 ,则b的值为_____.
,则b的值为_____.
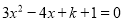 无实数根,化简:
无实数根,化简: