题目内容
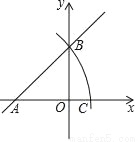
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=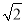 ,则b的值为_____.
,则b的值为_____.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,在平面直角坐标系中,直线y=x+b交x轴于点A,交y轴于点B,以点A为圆心,线段AB长为半径作圆弧,交x轴正半轴于点C,若AC=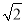 ,则b的值为_____.
,则b的值为_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案