题目内容
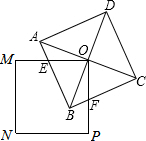 如图所示,已知正方形OPNM≌正方形ABCD,AC与BD交于点O,正方形OPNM绕O点旋转,OM交AB于E,OP交BC于F,如果正方形的边长为3,求四边形OEBF的面积.
如图所示,已知正方形OPNM≌正方形ABCD,AC与BD交于点O,正方形OPNM绕O点旋转,OM交AB于E,OP交BC于F,如果正方形的边长为3,求四边形OEBF的面积.考点:全等三角形的判定与性质,正方形的性质
专题:计算题
分析:根据正方形的性质,易证得△AOE≌△BOF,从而可知S四边形OEBF=S△AOB=
S正方形ABCD.
| 1 |
| 4 |
解答:解:∵∠AOE+∠BOE=90°,∠MOP=90°,
∴∠BOF=∠AOE,
在△OAE和△OBF中,
,
∴△AOE≌△BOF,
∴S△AOE=S△BOF.
∴S△AOE+S△OBE=S△BOF+S△OBE,
即S△AOB=S四边形OEBF,
∵S△AOB=
•OA•OB=
×
×
=
a2,
∴S四边形OEBF=
a2.
∴∠BOF=∠AOE,
在△OAE和△OBF中,
|
∴△AOE≌△BOF,
∴S△AOE=S△BOF.
∴S△AOE+S△OBE=S△BOF+S△OBE,
即S△AOB=S四边形OEBF,
∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| AB | ||
|
| AB | ||
|
| 1 |
| 4 |
∴S四边形OEBF=
| 1 |
| 4 |
点评:求解时需抓住正方形的特征,找出△AOE与△BOF在旋转过程中的对称性,获得四边形OEBF的面积与正方形面积的关系,关键是将四边形OEBF的面积转化为△OAB的面积.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
△ABC的三边长分别为
、
、2,△DEF的两边长分别为1和
,如果△ABC∽△DEF,那么△DEF的第三边长为( )
| 2 |
| 10 |
| 5 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、2
|
 如图,已知正方形ABCD,E为BC延长线上的一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G,连接AG,作FH⊥AG于H,交AD于I,连DH.
如图,已知正方形ABCD,E为BC延长线上的一点,连AE交CD于F,作∠AEG=∠AEB,EG交CD于G,连接AG,作FH⊥AG于H,交AD于I,连DH. 作图题:如图所示,将△ABC绕O点逆时针旋转60°后得到△DEF,请作出△DEF的图形.
作图题:如图所示,将△ABC绕O点逆时针旋转60°后得到△DEF,请作出△DEF的图形.