题目内容
△ABC的三边长分别为
、
、2,△DEF的两边长分别为1和
,如果△ABC∽△DEF,那么△DEF的第三边长为( )
| 2 |
| 10 |
| 5 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、2
|
考点:相似三角形的性质
专题:
分析:由△ABC的三边长分别为
、
、2,△DEF的两边长分别为1和
,如果△ABC∽△DEF,根据相似三角形的对应边成比例,即可求得答案.
| 2 |
| 10 |
| 5 |
解答:解:设△DEF的第三边长为x,
∵△ABC的三边长分别为
、
、2,△DEF的两边长分别为1和
,△ABC∽△DEF,
∴
=
=
,
解得:x=
.
即△DEF的第三边长为
.
故选C.
∵△ABC的三边长分别为
| 2 |
| 10 |
| 5 |
∴
| ||
| 1 |
| ||
|
| 2 |
| x |
解得:x=
| 2 |
即△DEF的第三边长为
| 2 |
故选C.
点评:此题考查了相似三角形的性质.此题比较简单,注意相似三角形的对应边成比例定理的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
多项式x2+y2、-x2+y2、-x2-y2、x2+(-y2)、8x2-y2、(y-x)3+(x-y)、2x2-
y2中,能在有理数范围内用平方差公式分解的有( )
| 1 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |
若|x-2|+|y+3|=0,则x+y( )
| A、0 | B、-1 | C、1 | D、-5 |
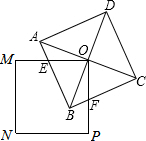 如图所示,已知正方形OPNM≌正方形ABCD,AC与BD交于点O,正方形OPNM绕O点旋转,OM交AB于E,OP交BC于F,如果正方形的边长为3,求四边形OEBF的面积.
如图所示,已知正方形OPNM≌正方形ABCD,AC与BD交于点O,正方形OPNM绕O点旋转,OM交AB于E,OP交BC于F,如果正方形的边长为3,求四边形OEBF的面积. 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|b|-|c|-|a+b|.
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,化简:|a|+|b|-|c|-|a+b|.