题目内容
已知(ab-2)2+| b-1 |
(1)a,b的值;
(2)
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2005)(b+2005) |
分析:(1)根据偶次方和算术平方根的非负性,可求a、b的值;
(2)把(1)求出的a、b的值代入找出简便方法即可.
(2)把(1)求出的a、b的值代入找出简便方法即可.
解答:解:(1)已知(ab-2)2+
=0,
∵(ab-2)2≥0,
≥0,
∴ab-2=0,b-1=0,
得:a=2,b=1;
(2)当a=2,b=1时,
+
+
+…+
=
+
+
+…+
=1-
+
-
+
-
+…-
+
-
=1-
=
.
| b-1 |
∵(ab-2)2≥0,
| b-1 |
∴ab-2=0,b-1=0,
得:a=2,b=1;
(2)当a=2,b=1时,
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2005)(b+2005) |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2006×2007 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2006 |
| 1 |
| 2006 |
| 1 |
| 2007 |
=1-
| 1 |
| 2007 |
=
| 2006 |
| 2007 |
点评:此题考查的知识点是非负数的性质,关键是根据非负性求出a、b的值,再代入求值.

练习册系列答案
相关题目
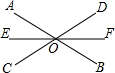 如图,已知直线AB、CD交于点O,OE平分∠AOC,OF平分∠BOD,
如图,已知直线AB、CD交于点O,OE平分∠AOC,OF平分∠BOD, 如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,求∠3的度数.
如图,已知直线AB、CD、MN相交于点O,∠1=22°,∠2=46°,求∠3的度数.