题目内容
15.计算(1)($\sqrt{12}$-4$\sqrt{\frac{1}{8}}$)-(3$\sqrt{\frac{1}{3}}$-4$\sqrt{0.5}$).
(2)(3$\sqrt{5}$-$\sqrt{12}$)($\sqrt{45}$+2$\sqrt{3}$)+(2$\sqrt{5}$+$\sqrt{125}$)÷(-$\sqrt{5}$)
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(2)先把各二次根式化为最简二次根式,然后利用平方差公式和二次根式的除法法则运算.
解答 解:(1)原式=2$\sqrt{3}$-$\sqrt{2}$-$\sqrt{3}$+2$\sqrt{2}$
=$\sqrt{3}$+$\sqrt{2}$;
(2)原式=(3$\sqrt{5}$-2$\sqrt{3}$)(3$\sqrt{5}$+2$\sqrt{3}$)+(2$\sqrt{5}$+5$\sqrt{5}$)÷(-$\sqrt{5}$)
=45-12+7$\sqrt{5}$÷(-$\sqrt{5}$)
=45-12-7
=26.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
5.下列计算正确的是( )
| A. | a4+a4=a8 | B. | 3(a-2b)=3a-2b | C. | a5÷a3=a2 | D. | (2a-b)2=4a2-b2 |
6.圆锥的高h、母线长l满足l=2h,底面半径为r,则其侧面展开图形的面积为( )
| A. | $\sqrt{2}$πh2 | B. | 2$\sqrt{3}$πh2 | C. | $\sqrt{3}$πhr2 | D. | πhr2 |
10.下列各数:$\frac{1}{3}$,π,$\root{3}{8}$,0,$\sqrt{3}$,其中无理数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
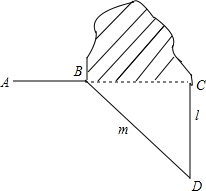 小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?
小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完? 如图,在长方形ABCD中,AC与BD相交于点O,DE∥AC,CE∥BD,那么△EDC可以看作是△OAB平移得到的,平移的距离是线段BC的长.
如图,在长方形ABCD中,AC与BD相交于点O,DE∥AC,CE∥BD,那么△EDC可以看作是△OAB平移得到的,平移的距离是线段BC的长.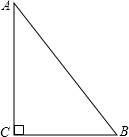 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.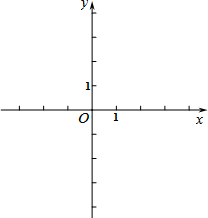 在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.
在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.