��Ŀ����
5����֪���ı���ABCD�У���A=x����C=y����0�㣼x��180�㣬0�㣼y��180�㣩����1����ABC+��ADC=360��-x-y���ú�x��y�Ĵ���ʽ��ʾ����
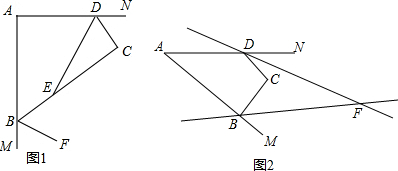
��2����ͼ1����x=y=90�㣬DEƽ�֡�ADC��BFƽ�����ABC���ڵ���ǣ���д��DE �� BF ��λ�ù�ϵ����˵�����ɣ�
��3����ͼ2����DFBΪ�ı���ABCD�ġ�ABC����ADC���ڵ����ƽ��������ֱ�߹��ɵ���ǣ�
�ٵ�x��yʱ����x+y=140�㣬��DFB=30������x��y��
��С������ͼʱ�����֡�DFB��һ�����ڣ���ֱ��ָ��x��y����ʲô����ʱ����DFB�����ڣ�
���� ��1�������ı����ڽǺͶ����ó��𰸼��ɣ�
��2�����ý�ƽ���ߵ����ʽ����������ǵ����ʵó����ɣ�
��3�������ý�ƽ���ߵ������Լ��������ڽǺͶ������ó���DFB=$\frac{1}{2}$y-$\frac{1}{2}$x=30�㣬�����ó�x��y��ֵ��
�ڵ�x=yʱ����ABC����ADC���ڵ����ƽ��������ֱ����ƽ�У���ʱ��DFB�����ڣ�
���  �⣺��1����ABC+��ADC=360��-x-y��
�⣺��1����ABC+��ADC=360��-x-y��
�ʴ�Ϊ��360��-x-y��
��2����ͼ1���ӳ�DE��BF��G
��DEƽ�֡�ADC��BFƽ�֡�MBC��
���CDE=$\frac{1}{2}$��ADC����CBF=$\frac{1}{2}$��CBM��
�֡ߡ�CBM=180��-��ABC=180��-��180��-��ADC��=��ADC��
���CDE=��CBF��
�֡ߡ�BED=��CDE+��C=��CBF+��BGE��
���BGE=��C=90�㣬
��DG��BF����DE��BF����
��3�����ɣ�1���ã���CDN+��CBM=x+y��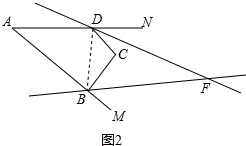
��BF��DF�ֱ�ƽ�֡�CBM����CDN��
���CDF+��CBF=$\frac{1}{2}$��x+y����
��ͼ2������DB�����CBD+��CDB=180��-y��
�á�FBD+��FDB=180��-y+$\frac{1}{2}$��x+y��=180��-$\frac{1}{2}$y+$\frac{1}{2}$x��
���DFB=$\frac{1}{2}$y-$\frac{1}{2}$x=30�㣬
�ⷽ���飺$\left\{\begin{array}{l}{x+y=140��}\\{\frac{1}{2}y-\frac{1}{2}x=30��}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=40��}\\{y=100��}\end{array}\right.$��
�ڵ�x=yʱ����ABC����ADC���ڵ����ƽ��������ֱ����ƽ�У���ʱ��DFB�����ڣ�
���� ������Ҫ�����˶���ε��ڽǺͽ�ƽ���ߵ������Լ��������ڽǺͶ�����֪ʶ����ȷӦ�ý�ƽ���ߵ������ǽ���ؼ���

 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�| A�� | 52 | B�� | 62 | C�� | 5 | D�� | 6 |
| A�� | -5 | B�� | -7 | C�� | 6 | D�� | -6 |
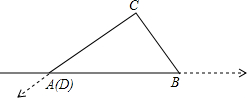 �������ϵ�A��B��C��D�ֱ��Ӧ��-3��7��13��21���������������ۺ�ʹ��D���A�غϣ�Χ��������ABC����ͼ��ʾ������sin��ABC��ֵΪ$\frac{4}{5}$��
�������ϵ�A��B��C��D�ֱ��Ӧ��-3��7��13��21���������������ۺ�ʹ��D���A�غϣ�Χ��������ABC����ͼ��ʾ������sin��ABC��ֵΪ$\frac{4}{5}$�� ��ͼ����������ABCD��һ���۵����ۺ�ΪAE����B��AD�ȡ�B��AE��24�㣬���B��EA=68�㣮
��ͼ����������ABCD��һ���۵����ۺ�ΪAE����B��AD�ȡ�B��AE��24�㣬���B��EA=68�㣮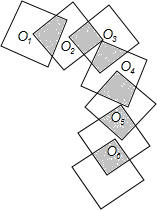 ��ͼ��7�������εı߳���Ϊ1��O1��O2��O3��O4��O5��O6��ǰ�����������ε����ģ�ͬʱ���Ǻ������������εĶ��㣬��ͼ����Ӱ���ֵ������1.5��
��ͼ��7�������εı߳���Ϊ1��O1��O2��O3��O4��O5��O6��ǰ�����������ε����ģ�ͬʱ���Ǻ������������εĶ��㣬��ͼ����Ӱ���ֵ������1.5��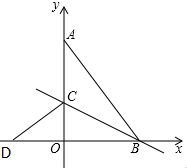 ��ͼ����ƽ��ֱ������ϵ�У���A��0��8����B��6��0��������AB������AOB�ع���B��ֱ���۵���ʹ��A����x���ϵĵ�D�����ۺ����ڵ�ֱ�߽�y���������ڵ�C����ֱ��DC�Ľ���ʽΪy=$\frac{3}{4}$x+3��
��ͼ����ƽ��ֱ������ϵ�У���A��0��8����B��6��0��������AB������AOB�ع���B��ֱ���۵���ʹ��A����x���ϵĵ�D�����ۺ����ڵ�ֱ�߽�y���������ڵ�C����ֱ��DC�Ľ���ʽΪy=$\frac{3}{4}$x+3��