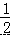题目内容
如图,已知在矩形ABCD中,AB = a,BC = b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
(1)若a = 5,sin∠ACB =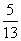 ,求的长。(3分)
,求的长。(3分)
(2)若a = 5,b=10当BE⊥AC时,求出此时AE的长.(4分)
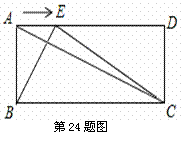 (3)设
(3)设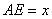 ,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.(5分)
,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.(5分)
解:(1)① b = 12 ……………………………3分
(2)如图1,∵BE⊥AC
∴∠2 + ∠3 = 900
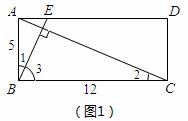 又∠1 + ∠3 = 900
又∠1 + ∠3 = 900
∴∠1 = ∠2
又∠BAE = ∠ABC = 900
∴△AEB ∽△BAC ………………………5分
∴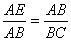 即
即 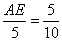
∴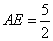 ………………………………7分
………………………………7分
(3)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC = 900
所以当△BAE ∽△CEB(如图2)
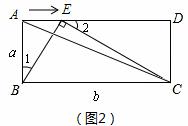 则∠1 = ∠BCE,
则∠1 = ∠BCE,
又BC∥AD
∴∠2 = ∠BCE
∴∠1 = ∠2
又∠BAE = ∠EDC = 900
∴△BAE ∽△EDC
∴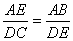 即
即 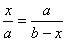
∴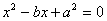 …………………………………9分
…………………………………9分
即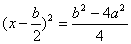
当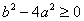
∵a>0,b>0, ∴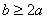
即 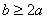 时,
时,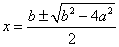 ……………………11分
……………………11分
综上所述:当a、b满足条件b = 2a时△BAE ∽△CEB,此时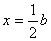 (或x = a);
(或x = a);
当a、b满足条件b>2a时△BAE ∽△CEB,此时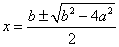


 的解是
的解是  ,求 a+b 的值.
,求 a+b 的值.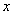 的一元二次方程
的一元二次方程 有一个实数根是2
有一个实数根是2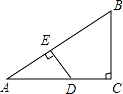
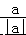 这四个数中,负数的个数( )
这四个数中,负数的个数( )