题目内容
在风速为24千米/小时的条件下,一架飞机顺风从A机场飞到B机场要用2.8小时,它逆风飞行同样的航线要用3小时,设无风时这架飞机在这一航线的平均速度为x千米/小时.
(1)飞机顺风飞行的速度为 千米/小时,逆风飞行的速度为 千米/小时
(2)求无风时这架飞机在这一航线的平均速度.
(1)飞机顺风飞行的速度为
(2)求无风时这架飞机在这一航线的平均速度.
考点:一元一次方程的应用
专题:
分析:(1)顺风飞行的速度=无风速度+风速,逆风速度=无风速度-风速,由此表示即可;
(2)设无风时飞机的航速是x千米/时,根据顺风速度×顺风时间=逆风速度×逆风时间,列出方程求出x的值.
(2)设无风时飞机的航速是x千米/时,根据顺风速度×顺风时间=逆风速度×逆风时间,列出方程求出x的值.
解答:解:(1)飞机顺风飞行的速度为x+24千米/小时,逆风飞行的速度为x-24千米/小时;
(2)设无风时飞机的航速是x千米/时,依题意得:
2.8×(x+24)=3×(x-24),
解得:x=696.
答:无风时飞机的航速是696千米/时.
(2)设无风时飞机的航速是x千米/时,依题意得:
2.8×(x+24)=3×(x-24),
解得:x=696.
答:无风时飞机的航速是696千米/时.
点评:此题考查了一元一次方程的应用,用到的知识点是顺风速度=无风时的速度+风速,逆风速度=无风时的速度-风速,关键是根据顺风飞行的路程等于逆风飞行的路程列出方程.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a+a=2a2 |
| B、a3×a4=a12 |
| C、(a3)2=a5 |
| D、(-a2)3=-a6 |
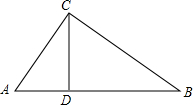 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6,BC=8,则CD等于( )
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC=6,BC=8,则CD等于( )A、
| ||
B、
| ||
| C、5 | ||
| D、4 |
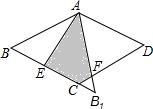 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为( )| A、0.7 | ||||
| B、0.9 | ||||
C、2
| ||||
D、
|
 图中有12个1×1的小正方形,它们共有20个顶点,从中取出3个,作为三角形的顶点,问:这些三角形中,面积是2的有多少个?
图中有12个1×1的小正方形,它们共有20个顶点,从中取出3个,作为三角形的顶点,问:这些三角形中,面积是2的有多少个?