题目内容
已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;

(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时求∠MON的大小;

(3)在(2)的条件下,若∠AOB=10°,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM:∠DON=2:3,求t的值.
分析:(1)因为∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.若OM平分∠AOB,ON平分∠BOD,则∠MOB=
∠AOB,∠BON=
∠BOD.然后根据关系转化求出角的度数;
(2)利用各角的关系求解:∠MON=∠MOC+∠BON-∠BOC=
∠AOC+
∠BOD-∠BOC=
(∠AOC+∠BOD)-∠BOC;
(3)由题意得∠AOM=
(10°+2t+20°),∠DON=
(160°-10°-2t),由此列出方程求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用各角的关系求解:∠MON=∠MOC+∠BON-∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由题意得∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)因为∠AOD=160°OM平分∠AOB,ON平分∠BOD
所以∠MOB=
∠AOB,∠BON=
∠BOD
即∠MON=∠MOB+∠BON=
∠AOB+
∠BOD=
(∠AOB+∠BOD)
=
∠AOD=80°;
(2)因为OM平分∠AOC,ON平分∠BOD
所以∠MOC=
∠AOC,∠BON=
∠BOD
即∠MON=∠MOC+∠BON-∠BOC=
∠AOC+
∠BOD-∠BOC
=
(∠AOC+∠BOD)-∠BOC
=
×180-20=70°;
(3)∵∠AOM=
(10°+2t+20°),∠DON=
(160°-10°-2t),
又∠AOM:∠DON=2:3,
∴3(30°+2t)=2(150°-2t)
得t=21.
答:t为21秒.
所以∠MOB=
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=∠MOB+∠BON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
(2)因为OM平分∠AOC,ON平分∠BOD
所以∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=∠MOC+∠BON-∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
(3)∵∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
又∠AOM:∠DON=2:3,
∴3(30°+2t)=2(150°-2t)
得t=21.
答:t为21秒.
点评:根据角平分线定义得出所求角与已知角的关系转化,然后根据已知条件求解.

练习册系列答案
相关题目
 若∠AOB=∠COD=
若∠AOB=∠COD=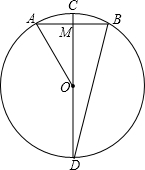 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD; 如图:在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=60°,AC=16,则图中长度为8的线段有
如图:在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=60°,AC=16,则图中长度为8的线段有 如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;
如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD=16,AB=8,求证:(1)BD2=DM•CD;