Question

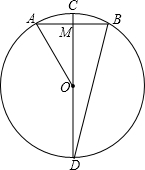如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD=16，AB=8，求证：（1）BD²=DM•CD；
（2）求∠D的度数；
（3）用扇形AOD围成一个圆锥，求此圆锥底面半径r的长．

Answer 1

分析：（1）可以证明△BDC∽△MDB，根据相似三角形的对应边的比相等即可证明；
（2）解Rt△OMB，即可求得∠AOM的度数，再根据圆周角定理即可求解；
（3）求得弧AD的弧长，即圆锥的底面圆周长，根据圆的周长公式即可求得半径．

解答：证明：（1）连接BC，
∵CD是直径，
∴∠DBC=90°，（1分）
∵CD⊥AB，
∴∠DMB=90°，
∵∠BDC=∠MDB，
∴△BDC∽△MDB，（2分）
∴

BD

MD

=

DC

BD

，
∴BD²=DM•CD；（4分）

（2）解：连接OB，则OB=OD=OC=

1

2

CD=

1

2

×16=8，（4分）
∵CD是直径，CD⊥AB，
∴BM=

1

2

AB=

1

2

×8=4，（6分）
在Rt△OMB中，sin∠BOM=

BM

OB

=

4

8

=

1

2

，
∴∠BOM=30°，
∴∠D=

1

2

∠BOM=

1

2

×30°=15°；（9分）

（3）解：由⊙O关于直径CD轴对称知：∠AOD=∠BOD=180°-30°=150°，（10分）
∴弧AD的长度

AD

l=

150×π×8

180

=

20

3

π，（11分）
由扇形弧长等于所围成圆锥底面圆的周长可得：

20

3

π=2π•r，
解得：r=

10

3

，
所以用扇形AOD围成的圆锥底面半径r为

10

3

．（12分）

点评：本题主要考查了相似三角形的性质，垂径定理以及圆锥的侧面展开图，正确解直角三角形求得∠BOM的度数是解题的关键．