题目内容
18.已知关于x的方程x2-2x-m=0没有实数根,那么m的取值范围是m<-1.分析 根据根的判别式得出b2-4ac<0,代入求出不等式的解集即可得到答案.
解答 解:∵关于x的方程x2-2x-m=0没有实数根,
∴b2-4ac=(-2)2-4×1×(-m)<0,
解得:m<-1,
故答案为:m<-1.
点评 本题主要考查对根的判别式,解一元一次不等式等知识点的理解和掌握,能根据题意得出(-2)2-4×1×(-m)<0是解此题的关键.

练习册系列答案
相关题目
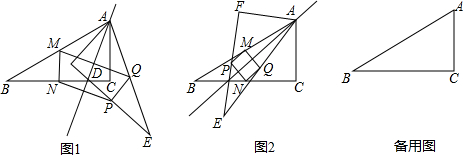
9. 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点m(3,3)为圆心,3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移,当直线l与圆m相切时,则运动的时间为( )| A. | 2.5 | B. | 5-2$\sqrt{2}$ | C. | 2.5或10 | D. | 5-2$\sqrt{2}$或5+2$\sqrt{2}$ |
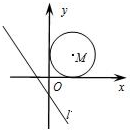
6.某商场三月份销售某品牌电视机,统计了其中三种型号电视机的销售量如下表显示:
根据本月各种型号电视机的销售全额和各种型号电视机的单价(销售全额=销售量×单价),制作了如下所示的统计图
由图解答下列问题:
(1)求该商场三月份销售这三种型号电视机的总销售金额;
(2)求出B,C两种型号电视机的销售单价,并把图②中的条形统计图补充完整;
(3)四月份,该商场三种电视机的销售单价不变,三种型号电视机共销出35台,已知A,B,C三种型号电视机销售数量的中位数是15台,总销售金额为98500元,求A,B,C三种型号电视机在四月份各销售了多少台?
| 电视机型号 | A型 | B型 | C型 |
| 销售量(台) | 5 | 10 | 20 |

由图解答下列问题:
(1)求该商场三月份销售这三种型号电视机的总销售金额;
(2)求出B,C两种型号电视机的销售单价,并把图②中的条形统计图补充完整;
(3)四月份,该商场三种电视机的销售单价不变,三种型号电视机共销出35台,已知A,B,C三种型号电视机销售数量的中位数是15台,总销售金额为98500元,求A,B,C三种型号电视机在四月份各销售了多少台?
13.下列四边形中,是轴对称但不是中心对称的图形是( )
| A. | 矩形 | B. | 菱形 | C. | 平行四边形 | D. | 等腰梯形 |
7.下列运算正确的是( )
| A. | 2x2÷x2=2x | B. | (-$\frac{1}{2}$a2b)3=-$\frac{1}{6}$a6b3 | C. | 3x2+2x2=5x2 | D. | (x-3)2=x2-9 |
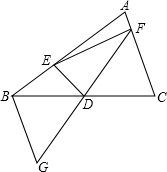 如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.
如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G.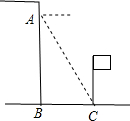 小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)
小丽在大楼窗口A测得校园内旗杆底部C的俯角为α度,窗口离地面高度AB=h(米),那么旗杆底部与大楼的距离BC=$\frac{h}{tanα}$米(用α的三角比和h的式子表示)