题目内容
20.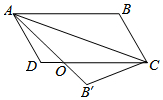 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交于点O.
(1)求证:OA=OC.
(2)过O点作OE⊥AC交AB于E点,连接CE,求证:四边形OAEC是菱形.
分析 (1)由在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,即可求得∠DCA=∠B′AC,则可证得OA=OC;
(2)根据折叠的性质和三角形的三线合一的性质得到AC与OE互相垂直平分即可证得结论.
解答 证明:(1)∵△AB′C是由△ABC沿AC对折得到的图形,
∴∠BAC=∠B′AC,
∵在平行四边形ABCD中,AB∥CD,
∴∠BAC=∠DCA,
∴∠DCA=∠B′AC,
∴OA=OC;
(2)O点作OE⊥AC交AB于E点,连接CE,
∵∠BAC=∠B′AC,OE⊥AC,
∴AC垂直平分OE,
∵OA=OC,
∴OE垂直平分AC,
∴AC与OE互相垂直平分,
∴四边形OCEA是菱形.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及折叠的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
11.|-1|的结果为( )
| A. | 1 | B. | ±1 | C. | -1 | D. | 无法确定 |
8.下列说法正确的是( )
| A. | 对角线互相垂直且相等的四边形是菱形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直的四边形是平行四边形 | |
| D. | 对角线相等且互相平分的四边形是矩形 |
5.设$\sqrt{10}$的小数部分为b,则b(b+3)的值是( )
| A. | 1 | B. | 是一个无理数 | C. | 3 | D. | 无法确定 |
 一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);
一天早上,马虎同学上学,到校后发现文具盒落在家里,此时离上课开始还有25分钟,于是立即步行回家取文具盒,同时,他爸爸从家里出发骑自行车以他3倍的速度给他送文具盒,两人在途中相遇,相遇后马虎立即坐父亲的自行车赶回学校.如图中线段AB、OB分别表示父子俩在送文具盒过程中,离学校的路程S(米)与所用时间t(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变);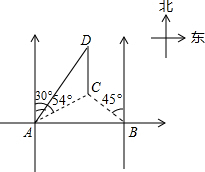 如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)