题目内容
12.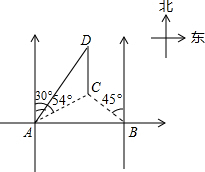 如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
如图,在海岸边相距12km的两个观测站A、B,同时观测到一货船C的方向角分别为北偏东54°和北偏西45°,该货船向正北航行,与此同时A观测站处派出一快艇以70km/h的速度沿北偏东30°方向追赶货船送上一批货物,正好在D处追上货船,求快艇追赶的时间.(参考数据:sin54°≈0.8,cos54°≈0.6,tan54°≈1.4)
分析 延长DC交AB于E,那么DE⊥AB,CE为直角△ACE和△CEB的公共直角边,可用CE表示出AE和EB,然后根据AB的长来求出CE的长,进而求得AE的长,那么就能在直角△ADE中,根据三角函数求出AD的长,即可求出时间.
解答 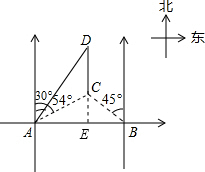 解:延长DC交AB于E,那么DE⊥AB.
解:延长DC交AB于E,那么DE⊥AB.
∵直角三角形ACE中,∠AEC=90°,∠ACE=54°,
∴AE=CE•tan54°≈1.4CE.
∵在直角三角形CEB中,∠BEC=90°,∠CBE=45°,
∴BE=CE.
∴AB=AE+BE=1.4CE+CE=12,
∴CE=5,
∴AE=1.4×5=7.
∵直角三角形ADE中,∠AED=90°,∠ADE=30°,
∴AD=AE÷sin30°=2AE=14.
因此快艇追赶的时间应该是14÷70=0.2小时.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
3.已知在一个样本中,40个数据分别落在4个组内,第一、二、四组数据个数分别为5、12、8,则第三组的频数为( )
| A. | 0.375 | B. | 0.6 | C. | 15 | D. | 25 |
17.某班九名同学在篮球场进行定点投篮测试,每人投篮五次,投中的次数统计如下:6,3,2,6,6,1,5,0,3,则这组数据的中位数、众数分别为( )
| A. | 3.6 | B. | 4.3 | C. | 3.3 | D. | 4.4 |
1.四个数-4,-2,0,1中最小的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 1 |
2.若kb>0,且不等式kx+b>0的解集是x<-$\frac{b}{k}$,则下列判断正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b<0 | D. | k<0,b>0 |
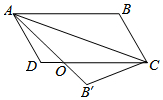 在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交
在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,AB′和CD相交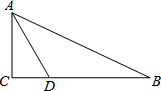 在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3.
在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3.