题目内容
10. 如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )
如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 利用切线的性质得直角△OAP,根据勾股定理求PA的长,由切线长定理可知:PA=PB=3$\sqrt{3}$.
解答 解:∵PA、PB分别切⊙O于点A、B,
∴PA=PB,∠OPA=90°,
在Rt△OAP中,∵OA=3,OP=6,
∴PA=$\sqrt{{6}^{2}-{3}^{2}}$=$\sqrt{36-9}$=3$\sqrt{3}$,
∴PB=PA=3$\sqrt{3}$,
故选C.
点评 本题考查了切线的性质和切线长定理,属于常考题型,要熟知圆的切线垂直于过切点的半径,明确过圆外一点,作圆的两条切线,切线长相等.

练习册系列答案
相关题目
5.定义运算$\frac{a}{b}$=$\frac{a+1}{b+1}$,若a≠-1,b≠-1,则下列等式中不正确的是( )
| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
2.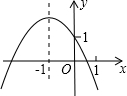 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
①b2-4ac>0;②a-b+c>1;③abc>0;④4a+2b+c<0;⑤c-a>1
其中,结论正确的有( )
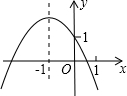 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①b2-4ac>0;②a-b+c>1;③abc>0;④4a+2b+c<0;⑤c-a>1
其中,结论正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
19.数轴上到原点的距离是$\sqrt{3}$的点表示的数是( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;
如图,在△ABC中,AC=4,D为BC上一点,CD=2,且△ADC与△ABD的面积比为1:3;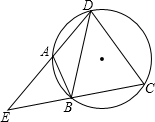 如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)
如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示) 如图,⊙O的半径为2,弦AB=2$\sqrt{3}$,OC⊥AB于点D,交⊙O于点C,则$\widehat{BC}$的长等于$\frac{4}{3}π$.
如图,⊙O的半径为2,弦AB=2$\sqrt{3}$,OC⊥AB于点D,交⊙O于点C,则$\widehat{BC}$的长等于$\frac{4}{3}π$.