题目内容
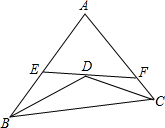 如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )
如图,BD,CD分别平分∠ABC,∠ACB,过点D作直线分别交AB,AC于点E,F,若AE=AF,BE=4,CF=2,则EF的长为( )| A、8 | ||
| B、6 | ||
C、2
| ||
D、4
|
考点:相似三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:利用三角形的内角和定理以及等腰三角形的性质,证明∠5=∠3,∠1=∠6,即可证明△BED∽△DFC.然后根据相似三角形的对应边的比相等求得.
解答: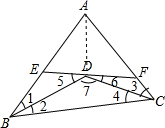 解:∵BD,CD分别平分∠ABC,∠ACB,
解:∵BD,CD分别平分∠ABC,∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵AE=AF,
∴∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴
=
,
连接AD,则DE=DF,
则ED2=CF•BE=2×4=8,
则ED=2
.
∴EF=2ED=4
.
 解:∵BD,CD分别平分∠ABC,∠ACB,
解:∵BD,CD分别平分∠ABC,∠ACB,∴∠1=∠2,∠3=∠4,
∵∠2+∠7+∠4=180°,∠5+∠6+∠7=180°,
∴∠2+∠4=∠5+∠6,即∠1+∠3=∠5+∠6,
∵AE=AF,
∴∠AEF=∠AFE,
∴∠1+∠5=∠3+∠6,
∴∠5=∠3,∠1=∠6,
∴△BED∽△CED,
∴
| ED |
| CF |
| BE |
| DF |
连接AD,则DE=DF,
则ED2=CF•BE=2×4=8,
则ED=2
| 2 |
∴EF=2ED=4
| 2 |
点评:本题考查了相似三角形的判定与性质以及等腰三角形的性质,正确证明∠5=∠3,∠1=∠6是关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 如图,在△ABC中,将边AB绕点B旋转60°至DB,将边AC绕点C旋转60°至EC,连结DA、EA、DC、EB,BE与CD相交于F,则下列结论不正确的是( )
如图,在△ABC中,将边AB绕点B旋转60°至DB,将边AC绕点C旋转60°至EC,连结DA、EA、DC、EB,BE与CD相交于F,则下列结论不正确的是( )| A、△ABD是等边三角形 |
| B、△ACE是等边三角形 |
| C、AF平分∠DFE |
| D、点F平分BE |
 如图,已知:△ABC中,BC=6.
如图,已知:△ABC中,BC=6.
 如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
如图,有甲、乙两建筑物,甲建筑物的高度为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.