题目内容
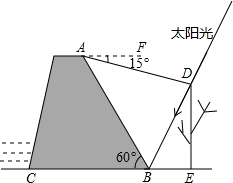 星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:
星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题
专题:
分析:利用题中所给的角的度数可得到△ABD中各角的度数,进而把已知线段AB整理到直角三角形中,利用相应的三角函数即可求得所求线段的长度.
解答:解:过D作DM⊥AB于M,
∵∠ABD=180°-∠ABC-∠DBE=60°,
∴在Rt△MBD中,
tan∠MBD=
=
,
设MB=x,则MD=
x,
∵AF∥CB,
∴∠FAB=∠ABC=60°,
∴∠DAM=∠FAM-∠FAD=45°,
在Rt△AMD中,
tan∠MAD=
=1,
∴AM=MD=
x,
∴
x+x=12,
∴x=6
-6,
在Rt△MBD中,cos∠MBD=
=
,
∴BD=2x=12
-12,
∵sin∠DBE=
=
,
∴DE=
(12
-12)≈7.6米,
答:这棵大树的高度约为7.6米.
∵∠ABD=180°-∠ABC-∠DBE=60°,
∴在Rt△MBD中,

tan∠MBD=
| MD |
| MB |
| 3 |
设MB=x,则MD=
| 3 |
∵AF∥CB,
∴∠FAB=∠ABC=60°,
∴∠DAM=∠FAM-∠FAD=45°,
在Rt△AMD中,
tan∠MAD=
| MD |
| MA |
∴AM=MD=
| 3 |
∴
| 3 |
∴x=6
| 3 |
在Rt△MBD中,cos∠MBD=
| MB |
| BD |
| 1 |
| 2 |
∴BD=2x=12
| 3 |
∵sin∠DBE=
| DE |
| BD |
| ||
| 2 |
∴DE=
| ||
| 2 |
| 3 |
答:这棵大树的高度约为7.6米.
点评:本题考查了解直角三角形-仰角的问题,解题的一般思路是通常把已知长度的线段整理到直角三角形中,利用公共边及相应的三角函数求解;所求的线段的长度也要进行代换,整理到相应的直角三角形中.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°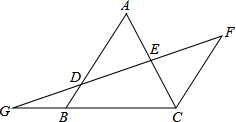 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图. 如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为
如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为
 如图,已知直线a∥b,∠1=120°,则∠2的度数是
如图,已知直线a∥b,∠1=120°,则∠2的度数是