题目内容
 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.(1)填空:A、C两港口间的距离为
(2)求图中点P的坐标;
(3)何时甲、乙两船相距20km.
考点:一次函数的应用
专题:
分析:(1)从图中可以看出A、C两港是30km,B、C两港是90km,A、C两港口间的距离为30+90=120km,求出甲的速度为,进而求出a的值120÷60=2,
(2)求出y1=60x-30,y2=30x,解出两个函数的交点,就是点P的坐标.
(3)先根据一次函数的图象求出甲及乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.
(2)求出y1=60x-30,y2=30x,解出两个函数的交点,就是点P的坐标.
(3)先根据一次函数的图象求出甲及乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.
解答:解:(1)从图中可以看出A、C两港是30km,B、C两港是90km,
∴A、C两港口间的距离为30+90=120km,
甲的速度为:30÷0.5=60
a的值,120÷60=2,
故答案为:120,2.
(2)由点(3,90)求得,y2=30x,
当x≥0.5时,由点(0.5,0),(2,90)求得,y1=60x-30,
当y1=y2时,60x-30=30x,
解得x=1,
此时y1=y2=30,
∴点P的坐标是(1,30).
(3)甲的速度为每小时60千米,
乙的速度为每小时30千米,
设x小时相距20千米,
第一种情况:60x-30x=30-20
解得x=
,
第二种情况:60x-30x=30+20
解得,x=
,
第三种情况,甲船停靠C港后,乙船继续航行,当乙船行70千米时,与甲船也相距20千米
所以时间为:70÷30=
.
∴A、C两港口间的距离为30+90=120km,
甲的速度为:30÷0.5=60
a的值,120÷60=2,
故答案为:120,2.
(2)由点(3,90)求得,y2=30x,
当x≥0.5时,由点(0.5,0),(2,90)求得,y1=60x-30,
当y1=y2时,60x-30=30x,
解得x=1,
此时y1=y2=30,
∴点P的坐标是(1,30).
(3)甲的速度为每小时60千米,
乙的速度为每小时30千米,
设x小时相距20千米,
第一种情况:60x-30x=30-20
解得x=
| 1 |
| 3 |
第二种情况:60x-30x=30+20
解得,x=
| 5 |
| 3 |
第三种情况,甲船停靠C港后,乙船继续航行,当乙船行70千米时,与甲船也相距20千米
所以时间为:70÷30=
| 7 |
| 3 |
点评:本题考查的是一次函数的图象及一次函数的应用,解答此题时要注意运用分类讨论的思想,不要漏解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
 如图,AB是⊙O的直径,C、D两点在⊙O上,且BC=CD,过点C作CE⊥AD,交AD的延长线于点E,交AB的延长线于点F.
如图,AB是⊙O的直径,C、D两点在⊙O上,且BC=CD,过点C作CE⊥AD,交AD的延长线于点E,交AB的延长线于点F.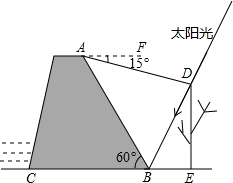 星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:
星期天,小强去水库大坝游玩,他站在大坝上的A处,看到一棵大树的影子刚好落在坝底的B处(假设大树DE与地面垂直,点A与大树及其影子在同一平面内),此时太阳光与地面成60°角;在A处测得树顶D的俯角为15°.如图所示,已知AB与地面的夹角为 60°,AB为12米.请你帮助小强计算一下这颗大树的高度?(结果精确到0.1米.参考数据:
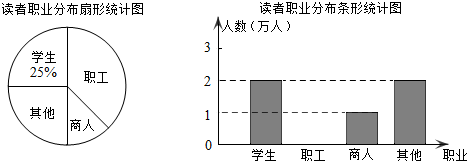
 列方程(组)解应用题:
列方程(组)解应用题:

 如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么
如图,点O在Rt△ABC的斜边AB上,⊙O切AC边于点E,切BC边于点D,连结OE,如果由线段CD、CE及劣弧ED围成的图形(阴影部分)面积与△AOE的面积相等,那么