题目内容
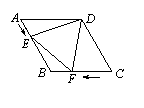
如图,在梯形ABCD中,AD∥BC,∠ADC=90°,∠B=30°,CE⊥AB,垂足为点E.若AD=1,AB=2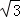 ,求CE的长.
,求CE的长.
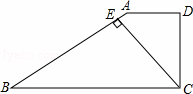
解:过点A作AH⊥BC于H,则AD=HC=1,
在△ABH中,∠B=30°,AB=2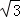 ,
,
∴cos30°= ,
,
即BH=ABcos30°=2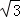 ×
× =3,
=3,
∴BC=BH+BC=4,
∵CE⊥AB,
∴CE= BC=2.
BC=2.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,AB=AC=5,sinB= ,⊙O过点B、C两点,且⊙O半径r=
,⊙O过点B、C两点,且⊙O半径r= ,则OA的值( )
,则OA的值( )
|
| A. | 3或5 | B. | 5 | C. | 4或5 | D. | 4 |
如图,在⊙O中,AB是直径,BC是弦,点P是 上任意一点.若AB=5,BC=3,则AP的长不可能为( )
上任意一点.若AB=5,BC=3,则AP的长不可能为( )

|
| A. | 3 | B. | 4 | C. |
| D. | 5 |

 .
. ,MD=4
,MD=4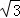 .
. 说明理由.
说明理由.