题目内容
对于平面直角坐标系中任意两点P1(x1,y1)、P2(x2,y2),称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离,记作:d(P1,P2).若P0(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P0,Q)的最小值为P0到直线y=kx+b的直角距离.令P0(2,﹣3).O为坐标原点.则:
(1)d(O,P0)= ;
(2)若P(a,﹣3)到直线y=x+1的直角距离为6,则a= .
5, 2或﹣10
解:(1)∵P0(2,﹣3).O为坐标原点,
∴d(O,P0)=|2﹣0|+|﹣3﹣0|=5.
故答案为:5;
(2)∵P(a,﹣3)到直线y=x+1的直角距离为6,
∴设直线y=x+1上一点Q(x,x+1),则d(P,Q)=6,
∴|a﹣x|+|﹣3﹣x﹣1|=6,即|a﹣x|+|x+4|=6,
当a﹣x≥0,x≥﹣4时,原式=a﹣x+x+4=6,解得a=2;
当a﹣x<0,x<﹣4时,原式=x﹣a﹣x﹣4=6,解得a=﹣10.
故答案为:2或﹣10.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
如图所示的立体图形,它的正视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
﹣ 的相反数是( )
的相反数是( )
|
| A. |
| B. | ﹣ | C. | 7 | D. | ﹣7 |




 有意义时,x的取值范围为
有意义时,x的取值范围为 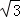 ,求CE的长.
,求CE的长.