��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������y=x2+bx+c�����㣨1����1�����ҶԳ���Ϊ����x=2����P��Q�����������ϣ���Pλ�ڶԳ����Ҳ࣬��Qλ�ڶԳ�����࣬PA��ֱ�Գ����ڵ�A��QB��ֱ�Գ����ڵ�B����QB=PA+1�����P�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�����ϵʽ��
��2�����Q�����꣨�ú�m��ʽ�ӱ�ʾ����
��3����̽��PA+QB=AB�Ƿ��������˵�����ɣ�
��4��������y=a1x2+b1x+c1��a1��0������Q��B��P���㣬����Գ�����ı���PAQB�ֳ����Ϊ1��5�������֣�ֱ��д����ʱm��ֵ��
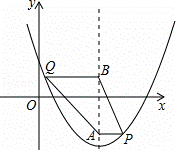
�⣺��1����������y=x2+bx+c�����㣨1����1�����ҶԳ���Ϊ����x=2��
��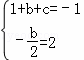 ��
��
���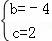 ��
��
����������������Ӧ�ĺ�����ϵʽy=x2��4x+2��
��2�����������ϵ�P�ĺ�����Ϊm��
��P��m��m2��4m+2����
��PA=m��2��
QB=PA+1=m��2+1=m��1��
���Q�ĺ�����Ϊ2����m��1��=3��m��
��Q����������3��m��2��4��3��m��+2=m2��2m��1��
���Q��������3��m��m2��2m��1����
��3��PA+QB=AB������
�������£���P��m��m2��4m+2����Q��3��m��m2��2m��1����
��A��2��m2��4m+2����B��2��m2��2m��1����
��AB=��m2��2m��1������m2��4m+2��=2m��3��
�֡�PA=m��2��QB=m��1��
��PA+QB=m��2+m��1=2m��3��
��PA+QB=AB��
��4����������y=a1x2+b1x+c1��a1��0������Q��B��P���㣬
��������y=a1x2+b1x+c1�ĶԳ���ΪQB�Ĵ�ֱƽ���ߣ�
�߶Գ�����ı���PAQB�ֳ����Ϊ1��5�������֣�
��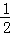 ��
��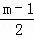 ��
��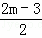 =
= ��
�� ��2m��3������2m��3����
��2m��3������2m��3����
�������2m��3����m��3��=0��
�ߵ�Pλ�ڶԳ����Ҳ࣬
��m��2��
��2m��3��0��
��m��3=0��
���m=3��

������̰������ѧ�̲���ʹ�õ�ij�ּ��������м��㣬���Ľ��Ϊ��������

| �� | A�� | 21 | B�� | 15 | C�� | 84 | D�� | 67 |
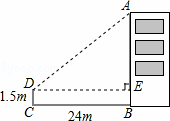
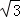 ����CE�ij���
����CE�ij���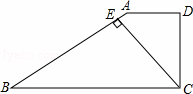

 B��
B��  C��
C��  D��
D�� 
 C. 4��108 D. 0.4��107
C. 4��108 D. 0.4��107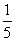 ����ô�ڴ�������ܸ���Ϊ_
����ô�ڴ�������ܸ���Ϊ_ ___________.
___________.