题目内容
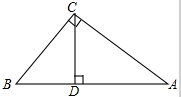如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AC=2| 3 |
考点：解直角三角形
专题：
分析：先证明Rt△ACD∽Rt△ABC，利用相似比得到2
：（AD+1）=AD：2
，整理得AD2+AD-12=0，解得AD=3或AD=-4（舍去），则AB=AD+BD=4，再在Rt△ABC中，利用余弦的定义可求出∠A的度数，然后根据含30度的直角三角形三边的关系求BC的长．
| 3 |
| 3 |
解答：解：∵CD⊥AB，
∴∠CDA=90°，
∵∠CAD=∠BAC，
∴Rt△ACD∽Rt△ABC，
∴AC：AB=AD：AC，即2
：（AD+1）=AD：2
，
整理得AD2+AD-12=0，解得AD=3或AD=-4（舍去），
∴AB=AD+BD=3+1=4，
在Rt△ABC中，∵cosA=
=
=
，
∴∠A=30°，
∴BC=
AB=2．
答：∠A=30°，BC=2，AB=4．
∴∠CDA=90°，
∵∠CAD=∠BAC，
∴Rt△ACD∽Rt△ABC，
∴AC：AB=AD：AC，即2
| 3 |
| 3 |
整理得AD2+AD-12=0，解得AD=3或AD=-4（舍去），
∴AB=AD+BD=3+1=4，
在Rt△ABC中，∵cosA=
| AC |
| AB |
2
| ||
| 4 |
| ||
| 2 |
∴∠A=30°，
∴BC=
| 1 |
| 2 |
答：∠A=30°，BC=2，AB=4．
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．
练习册系列答案
相关题目
如图，半径为5cm的圆中，圆心到弦AB的距离OE的长为4cm，则弦AB的长是（ ）| A、3cm | B、4cm |
| C、5cm | D、6cm |
设a、b是任意两个实数，且a＜b．我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当a≤x≤b时，有a≤y≤b，我们就称此函数是闭区间[a，b]上的“闭函数”．若二次函数y=
x2-2x是区间[m，n]上的“闭函数”，则实数m、n值分别为（ ）
| 1 |
| 2 |
A、m=1-
| ||||
B、m=-1，n=2或m=1-
| ||||
| C、m=-2，n=6 | ||||
D、m=-2，n=6或m=1-
|
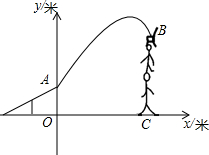杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，