题目内容
修建一段360米长的高速公路,甲工程队单独修建比乙工程队修建多10天,甲工程队比乙工程队每天少修6米,甲工程队每天修建费用是2万元,乙工程队每天修建费用是3.2万元.
(1)求甲乙两工程队单独完成这项工程各需多少天?
(2)如要求15天完成,设甲、乙两队各做a、b天,请写出完成此项工程所需费用W(万元)的方程式(用含有a、b的代数式表示),并求当a取何正整数时能使总费用最少?最少费用多少?
(1)求甲乙两工程队单独完成这项工程各需多少天?
(2)如要求15天完成,设甲、乙两队各做a、b天,请写出完成此项工程所需费用W(万元)的方程式(用含有a、b的代数式表示),并求当a取何正整数时能使总费用最少?最少费用多少?
考点:分式方程的应用,一次函数的应用
专题:
分析:(1)设乙工程队单独完成这项工程各需x天,则甲工程队单独完成这项工程各需x+10天,根据甲工程队每天比乙工程队少修建6米可列方程求解.
(2)根据甲工程队所用的时间和乙工程队用的时间,然后求出钱数,进一步列出函数,根据函数的性质探讨最少费用即可.
(2)根据甲工程队所用的时间和乙工程队用的时间,然后求出钱数,进一步列出函数,根据函数的性质探讨最少费用即可.
解答:解:(1)设乙工程队单独完成这项工程各需x天,则甲工程队单独完成这项工程各需x+10天,
根据题意,得
-
=6,
整理,得x2+10x-600=0,
解得x1=20,x2=-30.
经检验:x1=20,x2=-30都是原方程的根,但x2=-30不符合题意,舍去.
∴x=20.
则x+10=30,
答:甲工程队单独完成这项工程各需30天,乙工程队单独完成这项工程各需20天.
(2)所需费用W=2a+3.2b,
由
+
=1,得出b=20-
a,
所以W=-
a+64,W随着a的增大而减小,
而甲乙合作需要的天数是1÷(
+
)=12,
要求15天完成,要使总费用最少,则a取最大为15时,W最小为62.
答:a取15时总费用最少,最少费用62万元.
根据题意,得
| 360 |
| x |
| 360 |
| x+10 |
整理,得x2+10x-600=0,
解得x1=20,x2=-30.
经检验:x1=20,x2=-30都是原方程的根,但x2=-30不符合题意,舍去.
∴x=20.
则x+10=30,
答:甲工程队单独完成这项工程各需30天,乙工程队单独完成这项工程各需20天.
(2)所需费用W=2a+3.2b,
由
| a |
| 30 |
| b |
| 20 |
| 2 |
| 3 |
所以W=-
| 2 |
| 15 |
而甲乙合作需要的天数是1÷(
| 1 |
| 20 |
| 1 |
| 30 |
要求15天完成,要使总费用最少,则a取最大为15时,W最小为62.
答:a取15时总费用最少,最少费用62万元.
点评:本题考查分式方程的应用以及一次函数的性质,关键是以天数做为等量关系列方程求解,分别求出天数,然后求出钱数,进一步探讨谁的费用少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
抛物线y=-
x2+3x-
的对称轴是( )
| 1 |
| 2 |
| 5 |
| 2 |
| A、x=3 | ||
| B、x=-3 | ||
| C、x=6 | ||
D、x=-
|
 如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )
如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
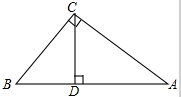 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2 如图,已知直角△ABC的两条边AC、AB的长分别为2
如图,已知直角△ABC的两条边AC、AB的长分别为2