题目内容
汽车在发动后的前10秒内以匀加速a=0.8m/s2行驶,这10s内,经过t(s)汽车行驶的路程为s=
at2
(1)求t=2.5s和3.5s时,汽车所行使的路程;
(2)汽车在发动后行驶10m、15m距离时所需的时间各为多少?(精确到0.1)
| 1 |
| 2 |
(1)求t=2.5s和3.5s时,汽车所行使的路程;
(2)汽车在发动后行驶10m、15m距离时所需的时间各为多少?(精确到0.1)
考点:函数值,算术平方根
专题:应用题
分析:(1)根据公式,可得函数解析式,根据自变量的值,可得函数值;
(2)根据函数值,可得相应的自变量的值.
(2)根据函数值,可得相应的自变量的值.
解答:解:(1)由题意s=
at2,得
s=
×0.8t2=
t2.
当t=2.5时,s=
×(2.5)2=2.5(m),
当t=3.5时,s=
×(3.5)2=5.9(m);
(2)当s=10时,
t2=10,解得t=5(s),
当s=15时,
t2=15,解得t≈6.1(s).
| 1 |
| 2 |
s=
| 1 |
| 2 |
| 2 |
| 5 |
当t=2.5时,s=
| 2 |
| 5 |
当t=3.5时,s=
| 2 |
| 5 |
(2)当s=10时,
| 2 |
| 5 |
当s=15时,
| 2 |
| 5 |
点评:本题考查了函数值,利用了函数的自变量与函数值的对应关系.

练习册系列答案
相关题目
 如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )
如图,△ABC的三个顶点均在正方形网格的格点上,则tanB的值为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
展开图中没有长方形的几何图形是( )
| A、正方形 | B、圆柱 | C、圆锥 | D、棱柱 |
 如图,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有弦中,长度为8的弦有( )
如图,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有弦中,长度为8的弦有( )| A、0条 | B、1条 | C、2条 | D、3条 |
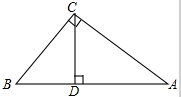 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2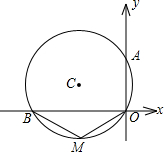 如图,圆心C经过坐标原点,与两坐标轴分别交于点B,A,点A的坐标为(0,4),M为劣弧
如图,圆心C经过坐标原点,与两坐标轴分别交于点B,A,点A的坐标为(0,4),M为劣弧