题目内容
 如图,半径为5cm的圆中,圆心到弦AB的距离OE的长为4cm,则弦AB的长是( )
如图,半径为5cm的圆中,圆心到弦AB的距离OE的长为4cm,则弦AB的长是( )| A、3cm | B、4cm |
| C、5cm | D、6cm |
考点:垂径定理,勾股定理
专题:
分析:如图,连接OB,证明AE=BE;根据勾股定理求出BE的长度问题即可解决.
解答: 解:如图,连接OB;
解:如图,连接OB;
∵OE⊥AB,
∴AE=BE;
由勾股定理得:
BE2=52-42=9,
∴BE=3,AB=2BE=6,
故选D.
 解:如图,连接OB;
解:如图,连接OB;∵OE⊥AB,
∴AE=BE;
由勾股定理得:
BE2=52-42=9,
∴BE=3,AB=2BE=6,
故选D.
点评:该题以圆为载体,以垂径定理、勾股定理等几何知识点的考查为核心构造而成;解题的关键是作辅助线,构造直角三角形,运用勾股定理等知识来分析、解答.

练习册系列答案
相关题目
抛物线y=-
x2+3x-
的对称轴是( )
| 1 |
| 2 |
| 5 |
| 2 |
| A、x=3 | ||
| B、x=-3 | ||
| C、x=6 | ||
D、x=-
|
展开图中没有长方形的几何图形是( )
| A、正方形 | B、圆柱 | C、圆锥 | D、棱柱 |
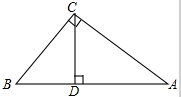 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2