题目内容
 杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,
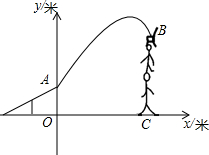
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一个点)的路线是抛物线,已知起跳点A距地面的高度为1米,弹跳的最大高度距地面4.75米,距起跳点A的水平距离为2.5米,建立如图所示的平面直角坐标系,
(1)求演员身体运行路线的抛物线的解析式?
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?说明理由.
考点:二次函数的应用
专题:
分析:(1)利用顶点式求出二次函数解析式即可;
(2)利用当x=4时,求出答案即可.
(2)利用当x=4时,求出答案即可.
解答:解:(1)如图所示:由题意可得抛物线的顶点坐标为:(2.5,4.75),且图象过(0,1),
故y=a(x-2.5)2+4.75,
则1=a(0-2.5)2+4.75,
解得:a=-
,
故y=-
(x-2.5)2+4.75,
=-
x2+3x+1;
(2)当x=4时,y=-
×42+3×4+1=3.4=BC,
故这次表演成功.
故y=a(x-2.5)2+4.75,
则1=a(0-2.5)2+4.75,
解得:a=-
| 3 |
| 5 |
故y=-
| 3 |
| 5 |
=-
| 3 |
| 5 |
(2)当x=4时,y=-
| 3 |
| 5 |
故这次表演成功.
点评:此题主要考查了二次函数的应用,正确求出二次函数解析式是解题关键.

练习册系列答案
相关题目
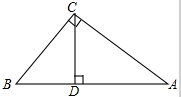 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AC=2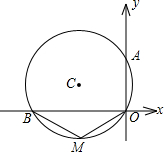 如图,圆心C经过坐标原点,与两坐标轴分别交于点B,A,点A的坐标为(0,4),M为劣弧
如图,圆心C经过坐标原点,与两坐标轴分别交于点B,A,点A的坐标为(0,4),M为劣弧