题目内容
如图,直线y=-x+4与两坐标轴分别相交于A、B点,点M(x,y)是直线AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由.
(2)设四边形OCMD面积S,求S与x的函数关系式;并求出当四边形OCMD为正方形时的面积.
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方形移动,这平移的距离为a(0<a<4),求当a为多少时正方形OCMD的周长被分为1:3.

(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由.
(2)设四边形OCMD面积S,求S与x的函数关系式;并求出当四边形OCMD为正方形时的面积.
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方形移动,这平移的距离为a(0<a<4),求当a为多少时正方形OCMD的周长被分为1:3.

考点:一次函数综合题
专题:
分析:(1)设点M的横坐标为x,则点M的纵坐标为-x+4,用坐标表示线段的长度则:MC=|-x+4|,MD=|x|,分成M在AB的延长线上,在线段AB上,在线段BA的延长线上,则x的范围即可确定,根据矩形的面积公式即可写出函数解析式;
(2)先用x表示出MC和MD的长,即可得到函数关系式;
(3)正方形OCMD的周长被分为1:3时,当A在直线AB的左侧时,如图(2),右侧是等腰直角三角形,等腰直角三角形的两直角边的和是矩形周长的
,据此即可求得;同理当A在直线AB的右侧时,如图(3),直线AB的左侧的部分是等腰直角三角形,等腰直角三角形的两直角边的和是矩形周长的
.
(2)先用x表示出MC和MD的长,即可得到函数关系式;
(3)正方形OCMD的周长被分为1:3时,当A在直线AB的左侧时,如图(2),右侧是等腰直角三角形,等腰直角三角形的两直角边的和是矩形周长的
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4,
则:MC=|-x+4|,MD=|x|,
当M在AB的延长线上时,即x<0时,则MC=|-x+4|=-x+4,MD=|x|=-x,
因而C四边形OCMD=2(MC+MD)=2(-x+4-x)=8-4x,此时四边形OCMD的周长是发生变化的;
当M在线段AB上时,即0<x<4,则MC=|-x+4|=-x+4,MD=|x|=x,
C四边形OCMD=2(MC+MD)=2(-x+4+x)=8,此时四边形OCMD的周长不发生变化;
当M在BA的延长线上,即x>4时,MC=|-x+4|=4-x,MD=|x|=x,
C四边形OCMD=2(MC+MD)=2(4-x+x)=8,此时四边形OCMD的周长不发生变化;
总之,当点M在线段AB上或BA的延长线上运动时,四边形OCMD的周长不发生变化,总是等于8.
当M在线段AB的延长线上时,四边形OCMD的周长发生变化;
(2)当M在AB的延长线上时,即x<0时,S=MC•MD=(-x+4)•(-x)=x2-4x;
当M在线段AB上时,0<x<4时,S=MC•MD=(-x+4)•x=-x2+4x;
当M在BA的延长线上,即x>4时,S=MC•MD=(4-x)•x=4x-x2;
当四边形OCMD为正方形时,P在线段AB上,此时-x+4=x,解得:x=2,
把x=2代入函数解析式S=MC•MD=(-x+4)•x=-x2+4x,得:S四边形OCMD=4,即四边形OCMD为正方形时的面积是4;
(3)当A在直线AB的左侧时,如图(2),右侧是等腰直角三角形,则正方形OCMD的周长被分为1:3时,2a=
×8,
解得:a=1.
当A在直线AB的右侧时,如图(3),直线AB的左侧的部分是等腰直角三角形,2(2+a-4)=
×8,
解得:a=3.
总之,a=1或3.
则:MC=|-x+4|,MD=|x|,
当M在AB的延长线上时,即x<0时,则MC=|-x+4|=-x+4,MD=|x|=-x,
因而C四边形OCMD=2(MC+MD)=2(-x+4-x)=8-4x,此时四边形OCMD的周长是发生变化的;
当M在线段AB上时,即0<x<4,则MC=|-x+4|=-x+4,MD=|x|=x,
C四边形OCMD=2(MC+MD)=2(-x+4+x)=8,此时四边形OCMD的周长不发生变化;
当M在BA的延长线上,即x>4时,MC=|-x+4|=4-x,MD=|x|=x,
C四边形OCMD=2(MC+MD)=2(4-x+x)=8,此时四边形OCMD的周长不发生变化;
总之,当点M在线段AB上或BA的延长线上运动时,四边形OCMD的周长不发生变化,总是等于8.
当M在线段AB的延长线上时,四边形OCMD的周长发生变化;
(2)当M在AB的延长线上时,即x<0时,S=MC•MD=(-x+4)•(-x)=x2-4x;
当M在线段AB上时,0<x<4时,S=MC•MD=(-x+4)•x=-x2+4x;
当M在BA的延长线上,即x>4时,S=MC•MD=(4-x)•x=4x-x2;
当四边形OCMD为正方形时,P在线段AB上,此时-x+4=x,解得:x=2,
把x=2代入函数解析式S=MC•MD=(-x+4)•x=-x2+4x,得:S四边形OCMD=4,即四边形OCMD为正方形时的面积是4;
(3)当A在直线AB的左侧时,如图(2),右侧是等腰直角三角形,则正方形OCMD的周长被分为1:3时,2a=
| 1 |
| 4 |
解得:a=1.
当A在直线AB的右侧时,如图(3),直线AB的左侧的部分是等腰直角三角形,2(2+a-4)=
| 1 |
| 4 |
解得:a=3.
总之,a=1或3.
点评:本题结合四边形的性质考查二次函数的综合应用,有关函数和几何图形的综合题目,要利用几何图形的性质和二次函数的性质把数与形有机地结合在一起,利用题中所给出的面积和周长之间的数量关系求解.

练习册系列答案
相关题目
 提出问题:怎么运用矩形面积表示(y+2)(y+3)与2y+5的大小关系(其中y>0)?
提出问题:怎么运用矩形面积表示(y+2)(y+3)与2y+5的大小关系(其中y>0)? 如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.
如图,在直角坐标系中,△ABC的顶点坐标是A(-1,2),B(-3,1),C(0,-1).将△ABC向右平移2个单位,向下平移3个单位得到△A1B1C1,将△A1B1C1绕O点旋转90°得到△A2B2C2.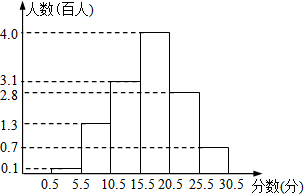 2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答:
2014年3月28日是第19人全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如图“频数分布直方图”.请回答: