题目内容
3．我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB的最小覆盖圆就是以线段AB为直径的圆．若在△ABC中，AB=AC，BC=6，∠BAC=120°，则△ABC的最小覆盖圆的半径是（ ）| A． | 3 | B． | $2\sqrt{3}$ | C． | 2 | D． | $3\sqrt{3}$ |
分析 作AD⊥BC于D，由等腰三角形的三线合一性质得出BD=CD=$\frac{1}{2}$BC=3，得出AD=$\sqrt{3}$，即可得出结果．
解答 解：作AD⊥BC于D，如图所示：则∠ADB=90°，
∵AB=AC，
∴BD=CD=$\frac{1}{2}$BC=3，∠B=∠C=30°，
∴AD=$\frac{\sqrt{3}}{3}$BD=$\sqrt{3}$＜3，
∴△ABC的最小覆盖圆的半径是BC边的一半=3，
故选：A．
点评 本题考查了三角形的最小覆盖圆；理解最小覆盖圆的定义是解决问题的关键．
练习册系列答案
相关题目
18．将一个半径为20的半圆纸片围成圆锥形纸筒，则圆锥的底面半径为（ ）
| A． | 10 | B． | 10$\sqrt{3}$ | C． | 20 | D． | 20$\sqrt{3}$ |
8．
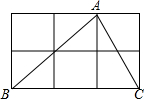如图，△ABC的3个顶点分别在小正方形的顶点上，这样的三角形叫做格点三角形，在图中再画格点三角形（位置不同于△ABC），使得所画三角形与△ABC全等，则这样的格点三角形能画（ ）
如图，△ABC的3个顶点分别在小正方形的顶点上，这样的三角形叫做格点三角形，在图中再画格点三角形（位置不同于△ABC），使得所画三角形与△ABC全等，则这样的格点三角形能画（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．在平面直角坐标系中，点P（-2，3）与点Q关于原点对称，则点Q的坐标为（ ）
| A． | （-2，-3） | B． | （3，-2） | C． | （2，3） | D． | （2，-3） |