题目内容
14.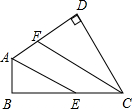 如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF.
如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF.
分析 先由四边形的内角和为360°,可得∠BAD+∠BCD=180°,然后由角平分线的定义可得:∠BAE+∠BCF=90°,然后由三角形内角和定理可得:∠BAE+∠BEA=90°,然后根据等量代换可得:∠BCF=∠BEA,从而根据同位角相等两直线平行,进而可证AE∥CF.
解答 解:∵∠B=∠D=90°,且∠B+∠D+∠BAD+∠BCD=360°,
∴∠BAD+∠BCD=180°,
∵AE、CF分别是∠DAB及∠DCB的平分线,
∴∠BAE+∠BCF=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠BCD=90°,
∵∠B+∠BAE+∠BEA=180°,
∴∠BAE+∠BEA=90°,
∴∠BCF=∠BEA,
∴AE∥CF.
点评 此题考查了平行线的判定,熟记同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,两直线平行是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
4.下列二次根式中,与$\sqrt{2}$不是同类二次根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{18}$ |
9.已知am=5,an=2,则am+n的值等于( )
| A. | 25 | B. | 10 | C. | 8 | D. | 7 |
19.下列四张扑克牌中,属于中心对称的图形是( )
| A. |  红桃7 | B. |  方块4 | C. |  梅花6 | D. |  黑桃5 |
4.下列几何体的主视图、左视图、俯视图都相同的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.