题目内容
5. 如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.(1)如图,当点O在△ABC的外部时,求证:四边形DGFE是平行四边形;
(2)当点O在△ABC的内部时,要使四边形DGFE是正方形,那么AO与BC必须满足什么关系?(直接写出答案,不需要说明理由)
分析 (1)利用三角形中位线定理得出DE∥GF且DE=GF,进而得出四边形DGFE是平行四边形;
(2)利用正方形的判定方法邻边相等的矩形是正方形得出即可.
解答  (1)证明:如图1,
(1)证明:如图1,
∵点D、E分别是AB、AC边的中点,
∴DE∥BC,且DE=$\frac{1}{2}$BC.
同理GF∥BC,且GF=$\frac{1}{2}$BC,
∴DE∥GF且DE=GF,
∴四边形DEFG是平行四边形.
(2)解:如图2,当OA=BC且OA⊥BC时,平行四边形DEFG是正方形, .
.
点评 此题主要考查了平行四边形的判定以及正方形的判定等知识,熟练掌握正方形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若xa+2+yb-1+3=0是关于x,y的二元一次方程,则a、b的值为( )
| A. | a=-1,b=2 | B. | a=-1,b=1 | C. | a=1,b=1 | D. | a=1,b=2 |
20.某校有300名学生参加毕业考试,其数学成绩在100-110分之间的有180人,则在100-110分之间的频率是( )
| A. | 0.6 | B. | 0.5 | C. | 0.3 | D. | 0.1 |
10.某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价),这两种服装的进价,标价如表所示.
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
| 类型 价格 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
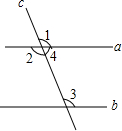 如图所示,已知直线a、b被直线c所截,以下结论:
如图所示,已知直线a、b被直线c所截,以下结论: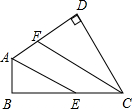 如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF.
如图,已知在四边形ABCD中,AE、CF分别是∠DAB及∠DCB的平分线,∠B=∠D=90°,求证:AE∥CF.