题目内容
18. 如图所示,AB=AC,点D,E分别在AC,AB上,AF⊥CE,AG⊥BD,垂足分别为F,G,AF=AG,下列结论:①∠B=∠C;②∠EAF=∠DAG;③AD=AE;④BE=CD
如图所示,AB=AC,点D,E分别在AC,AB上,AF⊥CE,AG⊥BD,垂足分别为F,G,AF=AG,下列结论:①∠B=∠C;②∠EAF=∠DAG;③AD=AE;④BE=CD其中正确的是①②③④(只填序号)
分析 根据HL可证Rt△AGB≌Rt△AFC,从而得出∠B=∠C,进而得出∠EAF=∠DAG,再利用ASA证明△AEF≌△AGD,从而得出AD=AE,BE=CD.
解答 解:∵AG⊥BD,AF⊥CE,
∴△AGB和△AFC是直角三角形,
在Rt△AGB和Rt△AFC中,
$\left\{\begin{array}{l}{AB=AC}\\{AG=AF}\end{array}\right.$,
∴Rt△AGB≌Rt△AFC(HL),
∴∠B=∠C,∠BAG=∠CAF,故①正确;
又∵∠BAG=∠EAF+∠FAG,∠CAF=∠DAG+∠FAG,
∴∠EAF=∠DAG,故②正确;
在△AFE和△AGD中,
$\left\{\begin{array}{l}{∠AFE=∠AGD}&{\;}\\{AF=AG}&{\;}\\{∠EAF=∠DAG}&{\;}\end{array}\right.$,
∴△AFE≌△AGD(ASA),
∴AD=AE,故③正确;
∵AB=AC,
∴AB-AE=AC-AD,
∴BE=CD,故④正确.
故答案为:①②③④.
点评 本题主要考查了直角三角形全等的判定与性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
6.如果一元二次方程x2-ax+6=0经配方后,得(x+3)2=3,则a的值为( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
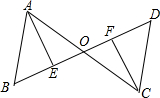 学了三角形全等的知识后,老师提出了一个问题.如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.那么△AOE和△COF全等吗?△AOB和△COD全等吗?请说明理由.
学了三角形全等的知识后,老师提出了一个问题.如图所示,点E、F在线段BD上,线段AC与BD互相平分,且BE=DF.那么△AOE和△COF全等吗?△AOB和△COD全等吗?请说明理由. 如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时:
如图,已知A(-2,0),B(0,-4),C(1,1),点P为线段OB上一动点(不包括点O),CD⊥CP交x轴于点D,当P点运动时: