题目内容
1．
已知，如图，AB∥CD，AD交BC于点O，EF过点O，分别交AB，CD于点E，F，且AE=DF．求证：O是EF的中点．
分析 由AB∥CD，可证得∠A=∠D，又由AE=DF，对顶角相等，即可利用AAS判定△AOE≌△DOF，继而证得结论．
解答 证明：∵AB∥CD，
∴∠A=∠D，
在△AOE和△DOF中，
$\left\{\begin{array}{l}{∠A=∠D}\\{∠AOE=∠DOF}\\{AE=DF}\end{array}\right.$，
∴△AOE≌△DOF（AAS），
∴OE=OF，
即O是EF的中点．
点评 此题考查了全等三角形的判定与性质．注意证得△AOE≌△DOF是解此题的关键．
练习册系列答案
相关题目
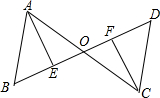学了三角形全等的知识后，老师提出了一个问题．如图所示，点E、F在线段BD上，线段AC与BD互相平分，且BE=DF．那么△AOE和△COF全等吗？△AOB和△COD全等吗？请说明理由．
如图，已知AE⊥BC，DF⊥BC，E、F是垂足，AE=DF，AB=DC．求证：AC=DB．
如图，已知A（-2，0），B（0，-4），C（1，1），点P为线段OB上一动点（不包括点O），CD⊥CP交x轴于点D，当P点运动时：