题目内容
14. 如图,四边形ABCD中,AB∥CD,AB∥CD,AD∥BC,AC和BD交于点O.
如图,四边形ABCD中,AB∥CD,AB∥CD,AD∥BC,AC和BD交于点O.求证:OA=OC.
分析 由平行线的性质得出∠ABD=∠CDB,∠ADB=∠CBD,由ASA证明△ABD≌△CDB,得出对应边相等AD=CB,再由AAS证明△AOD≌△COB,得出对应边相等即可.
解答 证明:∵AB∥CD,AD∥BC,
∴∠ABD=∠CDB,∠ADB=∠CBD,
在△ABD和△CDB中,
$\left\{\begin{array}{l}{∠ABD=∠CDB}&{\;}\\{BD=DB}&{\;}\\{∠ADB=∠CBD}&{\;}\end{array}\right.$,
∴△ABD≌△CDB(ASA),
∴AD=CB,
在△AOD和△COB中,
$\left\{\begin{array}{l}{∠ADB=∠CBD}&{\;}\\{∠AOD=∠COB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△AOD≌△COB(AAS),
∴OA=OC.
点评 本题考查了平行线的性质、全等三角形的判定与性质;熟练掌握平行线的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
4.图1是用绳索织成的一片网的一部分,小明探索这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:
表中“☆”处应填的数字为17;根据上述探索过程,可以猜想V,F,E之间满足的等量关系为V+F-E=1;
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为V+F-E=1.

| 特殊网图 |  |  |  |  |
| 结点数(V) | 4 | 6 | 9 | 12 |
| 网眼数(F) | 1 | 2 | 4 | 6 |
| 边数(E) | 4 | 7 | 12 | ☆ |
如图2,若网眼形状为六边形,则V,F,E之间满足的等量关系为V+F-E=1.

4.为了了解2015年我县九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩,下列说法正确的是( )
| A. | 2015年我县九年级学生是总体 | |
| B. | 样本容量是1000 | |
| C. | 1000名九年级学生是总体的一个样本 | |
| D. | 每一名九年级学生是个体 |
 在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.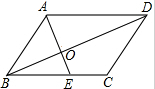 如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2.
如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2. 如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=40°,则∠BAE的度数为10°.
如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠C=40°,则∠BAE的度数为10°.