题目内容
 如图:AD为△ABC的中线,E为AD的中点,若∠DAC=∠B,CD=CE.试说明△ACE∽△BAD.
如图:AD为△ABC的中线,E为AD的中点,若∠DAC=∠B,CD=CE.试说明△ACE∽△BAD.考点:相似三角形的判定
专题:证明题
分析:先利用等腰三角形的性质,由CD=CE得到∠CED=∠EDC,则可根据等角的补角相等得到∠AEC=∠ADB,加上∠DAC=∠B,于是可根据有两组角对应相等的两个三角形相似判断△ACE∽△BAD.
解答:证明:∵CD=CE,
∴∠CED=∠EDC,
∵∠AEC+∠CED=180°,∠ADB+∠EDC=180°,
∴∠AEC=∠ADB,
∵∠DAC=∠B
∴△ACE∽△BAD.
∴∠CED=∠EDC,
∵∠AEC+∠CED=180°,∠ADB+∠EDC=180°,
∴∠AEC=∠ADB,
∵∠DAC=∠B
∴△ACE∽△BAD.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式正确的是( )
A、
| ||||
B、-
| ||||
| C、-0.1>-(-0.01) | ||||
| D、-π<-3.14 |
 如图,△ABC中,∠C=90°,AB=5,BC=3,CA=4,那么sinA等于( )
如图,△ABC中,∠C=90°,AB=5,BC=3,CA=4,那么sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知点(-1,y1),(2,y2),(3,y3)在二次函数y=x2-4x-5的图象上,则下列结论正确的是( )
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y3>y1>y2 |
| D、y2>y3>y1 |
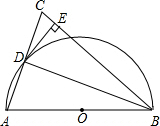 如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E.
如图,在△ABC中,BA=BC,以AB为直径作半圆⊙O,交AC于点D.连结DB,过点D 作DE⊥BC,垂足为点E. 如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.求证:AF=BE.
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.求证:AF=BE.