题目内容
9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a-2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由抛物线的开口方向、抛物线的对称轴以及抛物线与y轴的交点在y轴正半轴,即可得出a<0、b>0、c>0,进而可得出abc<0,结论①错误;②由当x=-1时,y=a-b+c<0,进而可得出a+c<b,结论②错误;③由当x=-2时,y=4a-2b+c<0,结论③错误;④由a+c<b、b=-2a,可得出2c<3b,结论④正确;⑤由抛物线的顶点坐标结合图形,可得出0≤m≤1,结论⑤正确.综上即可得出结论.
解答 解:①∵抛物线的对称轴为x=-$\frac{b}{2a}$=1,
∴b=-2a.
∵抛物线开口向下,
∴a<0,b>0.
∵抛物线与y轴的交点在y轴正半轴,
∴c>0,
∴abc<0,结论①错误;
②当x=-1时,y=a-b+c<0,
∴a+c<b,结论②错误;
③当x=-2时,y=4a-2b+c<0,
∴结论③错误;
④∵a+c<b,b=-2a,
∴c<b-a=$\frac{3}{2}$b,
∴2c<3b,结论④正确;
⑤∵抛物线的顶点坐标为(1,a+b+c),且a<0,
∴当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1,
∴结论⑤正确.
综上所述:正确的结论有④⑤.
故选B.
点评 本题考查了二次函数图象与系数的关系、二次函数的性质以及二次函数图象上点的坐标特征,观察函数图象,逐一分析五条结论的正误是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.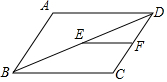 如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
 如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )| A. | 2.5 | B. | 3 | C. | 4 | D. | 3.5 |
 如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.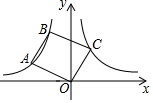 如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$.
如图,点A、B在双曲线y=$\frac{3}{x}$(x<0)上,连接OA、AB,以OA、AB为边作?OABC.若点C恰落在双曲线y=$\frac{2}{x}$(x>0)上,此时?OABC的面积为2$\sqrt{7}$. 若a,b,c在数轴上的位置如图所示,则|a-b|-|b-c|+|c-a|=0.
若a,b,c在数轴上的位置如图所示,则|a-b|-|b-c|+|c-a|=0.