题目内容
17.当0≤x≤2时,y=ax2+4(a+1)x-3在x=2时取得最大值,则实数a的取值范围是a$>-\frac{1}{2}$.分析 根据题意,可以分三种情况进行讨论,然后根据三种情况,从而可以得到a的取值范围.
解答 解:∵当0≤x≤2时,y=ax2+4(a+1)x-3在x=2时取得最大值,
∴当a>0时,a×22+4(a+1)×2-3>a×02+4(a+1)×0-3,
解得,a>$-\frac{2}{3}$,
∴a>0;
当a<0时,$\left\{\begin{array}{l}{a×22+4(a+1)×2-3>a×02+4(a+1)×0-3}\\{2≤-\frac{4(a+1)}{2a}}\end{array}\right.$,
解得,a$>-\frac{1}{2}$,
∴$-\frac{1}{2}<a<0$;
当a=0时,y=4x-3,则在当0≤x≤2时,y=4x-3在x=2时,取得最大值;
由上可得,实数a的取值范围是a$>-\frac{1}{2}$,
故答案为:a$>-\frac{1}{2}$.
点评 本题考查二次函数的最值,解答问题的关键是明确题意,利用分类讨论的数学思想解答,易错点是容易把a=0这种情况漏掉.

练习册系列答案
相关题目
8.在下列实数中,无理数是( )
| A. | $\root{3}{-27}$ | B. | -$\frac{5}{3}$ | C. | $\sqrt{0.01}$ | D. | 2π |
5.在下列实数中:1.57,-6,$\sqrt{2}$,0,π,$\sqrt{4}$,-3.030030003…,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列实数中,无理数是( )
| A. | $-\frac{2}{7}$ | B. | 0 | C. | $\sqrt{8}$ | D. | 3.14 |
9.下列约分中,正确的是( )
| A. | $\frac{x^2}{x^6}=\frac{1}{x^3}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a+b | ||
| C. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | D. | $\frac{x+1}{{x}^{2}-2x+1}$=$\frac{1}{x+1}$ |
 如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
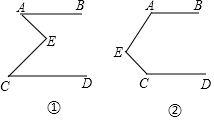 在图1和图2中,AB∥CD,你能说明∠A,∠E,∠C之间的数量关系吗?
在图1和图2中,AB∥CD,你能说明∠A,∠E,∠C之间的数量关系吗?