题目内容
17.已知a是$\sqrt{5}$的整数部分,b是$\sqrt{5}$的小数部分,求a+$\frac{1}{b+2}$的值.分析 首先对$\sqrt{5}$估算出大小,从而求出其整数部分a,再进一步表示出其小数部分b,代入即可解决问题.
解答 解:∵2$<\sqrt{5}$<3,
∴a=2,b=$\sqrt{5}$-2,
∴$\frac{1}{b+2}$=$\frac{1}{\sqrt{5}-2+2}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴a+$\frac{1}{b+2}$=2$+\frac{\sqrt{5}}{5}$=$\frac{10+\sqrt{5}}{5}$.
点评 此题主要考查了无理数的估算能力,用“夹逼法”正确的估算出无理数的大小,是解答此类题的关键.

练习册系列答案
相关题目
2.(-$\frac{1}{2}$)2001(-2)2000(-1)1999的正确答案( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
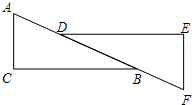 如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.
如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE. 如图,在△ABC中,BD是∠ABC的平分线,CD是∠ACE的平分线,试探索∠D与∠A的数量关系,并说明理由.
如图,在△ABC中,BD是∠ABC的平分线,CD是∠ACE的平分线,试探索∠D与∠A的数量关系,并说明理由. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G.连接AG.求证:△ABG≌△AFG.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G.连接AG.求证:△ABG≌△AFG. 如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=$\frac{BC}{CD}$;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的序号是①②③④.
如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=$\frac{BC}{CD}$;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的序号是①②③④. 如图所示,下列推理中正确的是( )
如图所示,下列推理中正确的是( )