题目内容
1.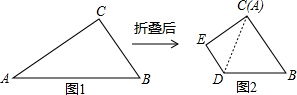 如图1,△ABC中,∠ACB=90°,AC=3$\sqrt{3}$,BC=3,将△ABC沿着一条直线折叠后,使点A与点C重合,如图2.
如图1,△ABC中,∠ACB=90°,AC=3$\sqrt{3}$,BC=3,将△ABC沿着一条直线折叠后,使点A与点C重合,如图2.(1)在如图1中画出折痕所在的直线l,设直线l与AB,AC分别相交于点D,E,连接CD(要求用尺规作图,不写作法,但保留作图痕迹)
(2)求证:△CDB是等边三角形;
(3)请你计算四边形EDBC的周长.
分析 (1)直线l是线段AC的垂直平分线,利用尺规即可作图;
(2)利用勾股定理求得BC的长,然后利用等角对等边证明CD=BD,求得CD的长度,根据等边三角形的定义证明;
(3)首先根据E是AC的中点求得CE的长,在直角△CDE中利用勾股定理求得DE的长,则四边形的周长即可求得.
解答 解:(1)如图所示: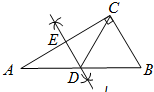 ;
;
(2)∵∠ACB=90°,AC=3$\sqrt{3}$,BC=3,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+{3}^{2}}$=6,
∵DE是AC的垂直平分线
∴AD=CD,
∴∠DAC=∠DCA,∠DAC+∠B=∠DCA+∠BCD=90°,∠B=∠BCD,CD=BD=AD=$\frac{1}{2}$AB=3,
CD=BD=BC.
(3)∵DE是AC的垂直平分线
∴AE=EC=$\frac{1}{2}$AC=$\frac{3\sqrt{3}}{2}$
∵CD=3,DE=$\sqrt{C{D}^{2}-E{C}^{2}}$=$\sqrt{(\sqrt{3})^{2}-(\frac{3\sqrt{3}}{2})^{2}}$=$\frac{3}{2}$,
四边形EDBC的周长=DE+EC+BC+DB=$\frac{3}{2}$+$\frac{3\sqrt{3}}{2}$+3+3=$\frac{15+3\sqrt{3}}{2}$.
点评 本题考查了线段的垂直平分线的性质以及勾股定理的应用,正确理解DE是垂直平分线是关键.

练习册系列答案
相关题目
12.我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
| 销售方式 | 批发 | 零售 |
| 利润(元/kg) | 6 | 12 |
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
6.如果将抛物线y=x2向右平移1个单位,那么所得的抛物线的表达式是( )
| A. | y=x2+1 | B. | y=x2-1 | C. | y=(x+1)2 | D. | y=(x-1)2 |
11. 如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB的度数为( )
如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB的度数为( )
 如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB的度数为( )
如图,⊙O是△ABC的外接圆,已知∠OAB=40°,则∠ACB的度数为( )| A. | 45° | B. | 40° | C. | 80° | D. | 50° |
 如图,在边长为2$\sqrt{3}$的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF=$\frac{\sqrt{3}}{2}$.
如图,在边长为2$\sqrt{3}$的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF=$\frac{\sqrt{3}}{2}$.