题目内容
12.我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:| 销售方式 | 批发 | 零售 |
| 利润(元/kg) | 6 | 12 |
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.
分析 (1)利用总利润=每千克利润×千克数列出函数解析式即可;
(2)根据题意求得x的取值范围,利用一次函数的性质求得答案即可.
解答 解:(1)由题意可知零售量为(2000-x)吨,故
y=6x+12(2000-x)
整理得y与x之间的函数关系式为y=-6x+24000.
(2)由题意得$\left\{\begin{array}{l}{x≥0}\\{2000-x≥0}\\{2000-x≤4x}\end{array}\right.$解得:400≤x≤2000.
∵-6<0,
∴y随x的增大而减小,
∴当x=400时,y有最大值,且y最大=21600元,
∴最大利润为21600元.
点评 此题考查一次函数的实际运用,掌握销售问题中的基本数量关系列出函数解析式是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
2.一件标价为a元的商品打9折后的价格是( )
| A. | (a-9)元 | B. | 90%a元 | C. | 10%a元 | D. | 9a元 |
3.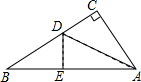 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
17.将抛物线y=x2向左平移1个单位,所得抛物线解析式是( )
| A. | y=(x-1)2 | B. | y=(x+1)2 | C. | y=x2+1 | D. | y=x2-1 |
 如图,已知线段AB=12,点C是AB的中点,点D是BC的中点,则线段CD=3.
如图,已知线段AB=12,点C是AB的中点,点D是BC的中点,则线段CD=3. 如图是一个正方体的表面展开图,则原正方体中与“祝”字所在的面相对的面上标的是利.
如图是一个正方体的表面展开图,则原正方体中与“祝”字所在的面相对的面上标的是利. 如图,∠BOA=90°,OC平分∠BOA,OA平分∠COD,求∠BOD的大小?
如图,∠BOA=90°,OC平分∠BOA,OA平分∠COD,求∠BOD的大小?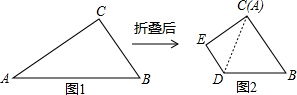 如图1,△ABC中,∠ACB=90°,AC=3$\sqrt{3}$,BC=3,将△ABC沿着一条直线折叠后,使点A与点C重合,如图2.
如图1,△ABC中,∠ACB=90°,AC=3$\sqrt{3}$,BC=3,将△ABC沿着一条直线折叠后,使点A与点C重合,如图2. 如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(1,4)和B(n,-2).
如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=$\frac{m}{x}$的图象交于点A(1,4)和B(n,-2).