题目内容
5. 在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.(1)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(2)在(1)条件下,当t为何值时,四边形EGFH为矩形.
(3)若G,H分别是折线A-B-C,C-D-A上的动点,与E,F相同的速度同时出发,当t为何值时,四边形EGFH为菱形.
分析 (1)由“两组对边分别相等的四边形是平行四边形”来判定;
(2)由“对角线相等的平行四边形是矩形”判定四边形EGFH为矩形时t的取值;
(3)首先,当四边形EGFH为菱形时,其对角线互相垂直且互相平分,在根据这一特点构造直角三角形,利用勾股定理求得t的对应的取值范围.
解答 解:(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,AD∥BC,∠B=90°,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,∠GAF=∠HCE,
∵G、H分别是AB、DC的中点,
∴AG=BG,CH=DH,
∴AG=CH,
∵AE=CF,
∴AF=CE,
在△AFG与△CEH中,$\left\{\begin{array}{l}{AG=CH}\\{∠GAF=∠HCE}\\{AF=CE}\end{array}\right.$
∴△AFG≌△CEH(SAS),
∴GF=HE
同理:GE=HF
∴四边形EGFH是平行四边形.
(2)解:如下图所示,连接GH,由(1)可知四边形EGFH是平行四边形
∵点G、H分别是矩形ABCD的边AB、DC的中点,
∴GH=BC=4,
∴当EF=GH=4时,四边形EGFH是矩形,分两种情况:
①AE=CF=t,EF=5-2t=4,
解得:t=0.5.
②AE=CF=t,EF=5-2(5-t)=4
解得:t=4.5
即:当t为0.5秒或4.5时,四边形EGFH为矩形

(3)如下图所示,连接AG、CH
∵如果四边形EGFH是菱形,
则必有EF⊥GH,OE=OF,OG=OH
∴易证△CAB∽△CGO
∴$\frac{AB}{OG}=\frac{AC}{CG}$
∴$\frac{3}{OG}=\frac{5}{7-t}$
∴OG=$\frac{21-3t}{5}$
又在Rt△ABG中,AB=3,BG=t-3,
∴AG2=(t-3)2+9,
∴在Rt△AGO中,(t-3)2+9=($\frac{5}{2}$)2+($\frac{21-3t}{5}$)2,
化简得:64t2-96t-589=0
(8t-6)2=625,
8t-6=±25
解得:t1=$\frac{31}{8}$或t2=-19(舍去)
即:当t为$\frac{31}{8}$秒时,四边形EGFH为菱形.
点评 本题考查了特殊四边形的判定、性质及综合应用,解题的关键是熟练掌握特殊四边形的性质、判定,具有应用代数的方法解决几何问题的意识.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 3a | B. | a | C. | 4a | D. | 都不对 |
 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年人组共有210人,则老年组共有30人.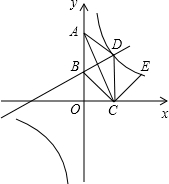 如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.
如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.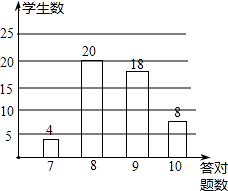 数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )
数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )