题目内容
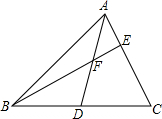 如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:(1)当
| AF |
| AD |
| 1 |
| 2 |
| AE |
| AC |
| 1 |
| 3 |
(2)当
| AF |
| AD |
| 1 |
| 3 |
| AE |
| AC |
| 1 |
| 5 |
(3)当
| AF |
| AD |
| 1 |
| 4 |
| AE |
| AC |
| 1 |
| 7 |
…
猜想:当
| AF |
| AD |
| 1 |
| n+1 |
| AE |
| AC |
考点:平行线分线段成比例,三角形中位线定理
专题:
分析:如图,作辅助线;证明
=
=
,得到EG=nAE;证明EG=CG,AC=(2n+1)AE,即可解决问题.
| AE |
| AG |
| AF |
| AD |
| 1 |
| n+1 |
解答: 解:猜想:当
解:猜想:当
=
时,
=
;理由如下:
如图,过点D作DG∥BE,交AC与点G;
则
=
=
,
∴
=
,EG=nAE;
∵AD是△ABC的中线,
∴EG=CG,AC=(2n+1)AE,
∴
=
.
 解:猜想:当
解:猜想:当| AF |
| AD |
| 1 |
| n+1 |
| AE |
| AC |
| 1 |
| 2n+1 |
如图,过点D作DG∥BE,交AC与点G;
则
| AE |
| AG |
| AF |
| AD |
| 1 |
| n+1 |
∴
| AE |
| EG |
| 1 |
| n |
∵AD是△ABC的中线,
∴EG=CG,AC=(2n+1)AE,
∴
| AE |
| AC |
| 1 |
| 2n+1 |
点评:该题主要考查了平行线分线断成比例定理等几何知识点的性质及其应用问题;解题的关键是作辅助线,构造平行线,灵活运用平行线分线断成比例定理来分析、判断、推理或解答.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
借助一副三角尺,你能画出的角的度数是( )
| A、65° | B、15° |
| C、85° | D、95° |
下列几何体中:正方体,长方体,圆柱,六棱柱,圆锥,球,截面的形状可以为长方形的个数为( )
| A、3个 | B、4 | C、5个 | D、6个 |
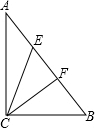 已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.
已知E、F是Rt△ABC斜边AB的三等分点,AE=EF=FB,且CE=4,CF=3,求斜边AB的长.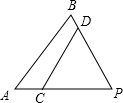 如图,在△PAB中,C,D分别为AP,BP上的点,若
如图,在△PAB中,C,D分别为AP,BP上的点,若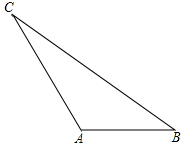 如图所示,在△ABC中,AB=1,AC=
如图所示,在△ABC中,AB=1,AC= 如图所示,在△ABC中,∠B=45°,∠C=30°,AB=4
如图所示,在△ABC中,∠B=45°,∠C=30°,AB=4