题目内容
17.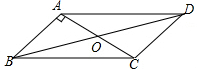 如图所示,?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BD=$\sqrt{5}$,则对角线BD=1.
如图所示,?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=1,BD=$\sqrt{5}$,则对角线BD=1.
分析 由平行四边形的性质得出OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD=$\frac{\sqrt{5}}{2}$,由勾股定理求出OA,即可得出对角线AC.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD=$\frac{\sqrt{5}}{2}$,
∵AB⊥AC,
∴∠BAO=90°,
∴OA=$\sqrt{O{B}^{2}-A{B}^{2}}$=$\sqrt{(\frac{\sqrt{5}}{2})^{2}-{1}^{2}}$=$\frac{1}{2}$,
∴AC=2OA=1;
故答案为:1.
点评 本题考查了平行四边形的性质、勾股定理;熟记平行四边形的性质,由勾股定理求出OA是解决问题的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知抛物线y=ax2+bx+c的开口向上,顶点坐标为(3,-2),那么该抛物线有( )
| A. | 最小值-2 | B. | 最大值-2 | C. | 最小值3 | D. | 最大值3 |
6.已知3x=5,9y=10,则3x+2y=( )
| A. | 50 | B. | -100 | C. | 100 | D. | 无法确定 |
16.设O是等边三角形ABC内一点,已知∠AOB=130°,∠BOC=125°,则在以线段OA,OB,OC为边构成的三角形中,内角不可能取到的角度是( )
| A. | 65° | B. | 60° | C. | 45° | D. | 70° |
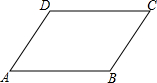 已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D.
已知:如图,AB∥CD,∠A=∠C,求证:∠B=∠D.